MMSD_Core

MMSD_Core package contains all core classes for MMSD project. More...

MMSD_Core package contains all core classes for MMSD project.

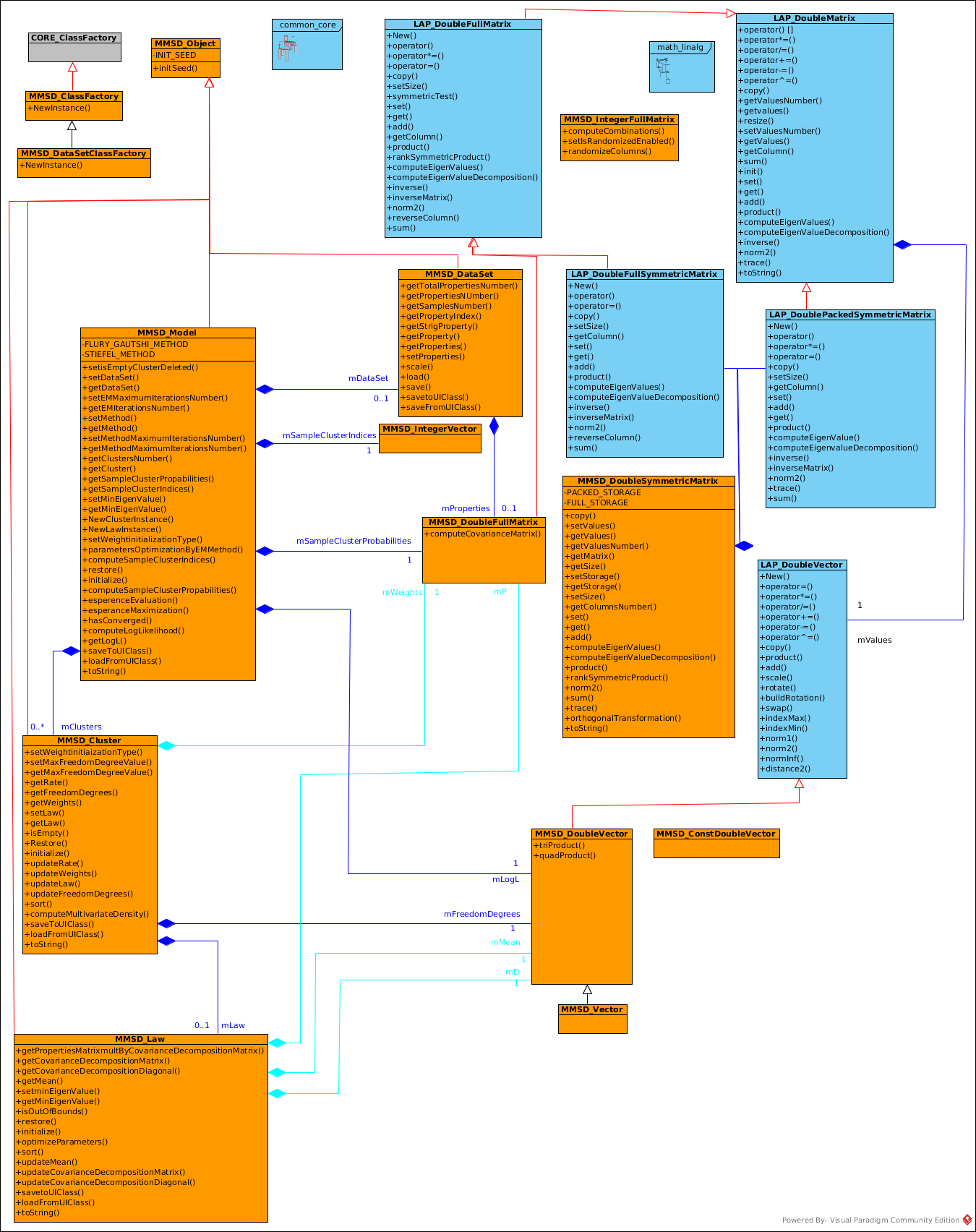
The most important class is the MMSD_Model which uses all the other classes.

MMSD_Model contains a data set MMSD_DataSet wich is a full matrix of size N x P where

• N is the number of samples (of size 10 000)
• P is the number of properties which can have a name of (size 10)

To each Model is associated a cluster (MMSD_Cluster) and to each cluster is associated a law (MMSD_Law) whose instances have to be created by a specialization of MMSD_Model. Some implementations are available in the package MMSD_Model.

A model MMSD_Model has: (N: number of samples)

• a list of clusters of size K
• a sample probability to be in cluster k in [0,K[ (matrix of size NxK)

A cluster MMSD_Cluster has (P: number of properties)

• weight for each sample property (matrix of size NxP )
• freedom degree for each properties (vector of size P)
• rate percent of samples in cluster in [0,1]
• an associated law

MMSD_Cluster needs the Gamma distribution function STAT_GammaDistribution defined in MATH_Statistics_Distributions package to perform its weight attribute array initialization in case of gamma of weight initialisation type MMSD_Cluster::setWeightInitializationType

A law MMSD_Law describes the cluster 's law. It has:

• a mean value of each properties (vector of size p)
• the property covariance matrix divided in 2 parts:
  • the eigen value decomposition diagonal matrix
  • the eigen value decomposition matrix

The eigen values & matrix vector or vector vector products are performed by BLAS/LAPACK library based of the package MATH_Linalg_Core

The main method is MMSD_Model::parametersOptimizationByEMMethod() with K,sampleClusters,backupPath,backupPrefix, nDigits,backupSteps parameters:

• K is the number of clusters to pack the data.
• sampleClusters is the initial cluster for each sample whose value is in [0,K[
• The other parameters are used to save the files during the process.

The algorithm of this method is as follow:

• step 1 initialization of the model MMSD_Model::initialize();
  • Input:
    • clusterIndex, an array of int of size N
    • propertisMatrix, the full data matrix of size NxP
    • K : the number of clusters
  • Output: create the list of K elements of MMSD_Cluster of the model: To each cluster:
    • a new law MMSD_Law is associated ,
    • the weight parameters of the cluster is set
    • the cluster is initialized: MMSD_Cluster::initialize() so that :
      • its normalized rate number (number of samples in the cluseter ) is computed
      • its freedom degre are initialized ith i an array of size P
      • its weight matrix of size NxP is initialized
      • its associated law is also initialize MMSD_Law::initialize() with the property matrix Y and the rate number. The initialization of the law consist in computing:
        • the extracted samples property matrix mYP of size nRates x P
        • the mean values mMean of size P of the properties at index p<P is computed for the extarcted samples
        • the covariance of Yp is computed and is used to compute its eigen value decomposition mD,mP: tP.D.P of size P in an desent order.
        • the eigen values is supposed not to be below a min tolerate eigen value
        • mYP:= Y.mP of size N x P
      • the list of index of cluster for each sample is stored in mSampleClusterIndices of size N
      • the propbality of the sample to be in cluster k is computed in mSampleClusterProbabilities by the method MMSD_Model::computeSampleClusterProbabilities of size NxK.

step 2: an esperance evlaution is computed MMSD_Model::esperanceEvaluation()

• step 3: maximizatio of this esperance MMSD_Model::esperanceMaximization()
• step 4: verification taht the computing give result not out of bounds MMSD_Law::isOutOfBounds()
• step 5: compute the log-likelihood function MMSD_Model::computeLogLikelihood() which must not be NaN.
• go to step 2 until the number of iterations is not reached

step 6: compute the finaly index of the cluter for each sample MMSD_Model::computeSampleClusterIndices()

The package contains the class:

• MMSD_Object which is the core class of all objects.
• MMSD_DoubleVector whith describes a real vector
• MMSD_IntegerVector which describes an integer vector
• MMSD_DoubleFullMatrix which describes a real matrix
• MMSD_DoubleSymmetricMatrix which describes symmetric matrix in various storage types.
• MMSD_DataSet which describes a data set defined by properties & groups
• MMSD_Model which describes a model
• MMSD_ClassFactory which describes a MMSD classes factory generator
• MMSD_DataSetClassFactory which describes a factory to instanciate MMSD_DataSet class.

The organization of this package is as follow: