The Revolution ellipsoide examples consists in studing an ellipsoide of diameters L,L,3.L in the canonical directions (x,y,z).

The matter parameters are as follow (Fer-Alpha type):

Ms	Aimantations (A/m)	1.7e6
K1	First Anisotropy (J/m^3)	4.8e5
K3	Secund Anisotropy (J/m^3)	1.5e5
A	Exchange (J/m^3)	2.1e-11

The domain is discretized in 64x64x64 cells.

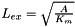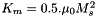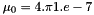The exchange length is $L_{ex}=\sqrt \frac{A}{K_m}$ where $K_m=0.5.\mu_0 M_s^2$ and $\mu_0=4.\pi 1.e-7$ .

We well make vary the length of the ellipsoide with respect of a multiple of Lex (2,1,0.5,0.25).

First, we choose L=2.Lex.

The length of the ellipsoide is 2.Lex, the mesh size is 1.0625e-10x1.0625e-10x3.1875e-10

The anisotropy direction U1 is uniformly in the Z-direction with a unaxial crystal type.

The initial magnetism M is uniformly in the Z direction.

The external magnetism field is set to null.

The geometry clipped in 2 orthogonal plan at origin:

matter in domain

The code to generate files:

microm_domain.exe --path=./ --output=./Data --prefix=revolutionEllipsoide-2 --geometry=DISK[3,0,0,0,.00000000680000000000,.00000000680000000000,3*.00000000680000000000] --mesh=[64,64,64] --nMatters=1 --ms=1700000.0 --k1=480000.0 --k3=150000.0 --a=.00000000002100000000 --alpha=0.5 --u=[0,0,1] --v=[0,0,0] --w=[0,0,0] --crystal=UNIAXIAL --Hinit=[0,0,1] make create

The code to compute the magnetism at equilibrium state :

microm_grid3d_openmp.exe --path=./Data --output=./Output --prefix=revolutionEllipsoide-2 --mesh=revolutionEllipsoide-2.geo --matter=revolutionEllipsoide-2.mat --anisotropy=revolutionEllipsoide-2.ani --with-anisotropy=false --with-exchange=true --with-demagnetized=true --with-magnetostriction=false --periodicity=[false,false,false] --nlevels=-1 --Hinit=revolutionEllipsoide-2.aim --Hext=[0,0,0] --iterations=25000 --tolerance=1.e-8 --nthreads=4 --profiling=false --verbose=./Output/revolutionEllipsoide-2.log make run

The relaxation technics converges in 5093 iterations and stops because of the variation of energy is less than 1.e-8.

The computation takes 5 hours.

The value of magnetism field at equilibrium state are plot as follow:


equilibrium magnetism value along x for L=2Lex	equilibrium magnetism value along y for L=2Lex	equilibrium magnetism value along z for L=2Lex


equilibrium magnetism vector with total magnetism module for L=2Lex	equilibrium total magnetism field norm for L=2Lex

When L=1.Lex, the mesh size is 5.3125e-11x 5.3125e-11x1.59375e-10.

The value of magnetism field at equilibrium state are plot as follow:


equilibrium magnetism value along x for L=Lex	equilibrium magnetism value along y for L=Lex	equilibrium magnetism value along z for L=Lex


equilibrium magnetism vector with total magnetism module for L=Lex	equilibrium total magnetism field norm for L=Lex

When L=0.25 Lex, the mesh size is 1.32812e-11 x 1.32812e-11 x 3.98437e-11

The value of magnetism field at equilibrium state are plot as follow:


equilibrium magnetism value along x for L=Lex/4	equilibrium magnetism value along y for L=Lex/4	equilibrium magnetism value along z for L=Lex/4


equilibrium magnetism vector with total magnetism module for L=Lex/4	equilibrium total magnetism field norm for L=Lex/4