The periodical cross tie examples consists in studing a thin sheet of permalloy considered as an infinite periodical sheet in the y-direction.
The first sheet is rectangular with 0.0015625 micron of width (Z direction) , 0.2 micron of height (Y direction) & 0.1 micron of length (X direction). The mesh contains 64 cells in X direction, 64 cells in Y direction & 4 cells in Z-direction. The cell 's size is 1.5625 x 3.125 x 0.390625 nm^3
The second sheet is rectangular with 0.0015625 micron of width (Z direction) , 0.2 micron of height (Y direction) & 0.1 micron of length (X direction). The mesh contains 64 cells in X direction, 128 cells in Y direction & 8 cells in Z-direction. The cell 's size is 1.5625 x 1.5625 x 0.195312 nm^3
The third sheet is rectangular with 0.0015625 micron of width (Z direction), 0.2 micron of height (Y direction) & 0.1 micron (X direction) of length in order to have cubic cell. The mesh contains 64 cells in X direction, 128 cells in Y direction & 1 cells in Z-direction. The cell 's size is 1.5625 x 1.5625 x 1.5625 nm^3
The fourth sheet is rectangular with 0.0015625 micron of width (Z direction), 0.2 micron of height (Y direction) & 0.1 micron (X direction) of length in order to have cubic cell. The mesh contains 256 cells in X direction, 512 cells in Y direction & 4 cells in Z-direction. The cell 's size is 0.390625 x 0.39625 x 0.390625 nm^3
The anisotropy direction U1 is uniformly in the Y-direction with uniaxial crystal type
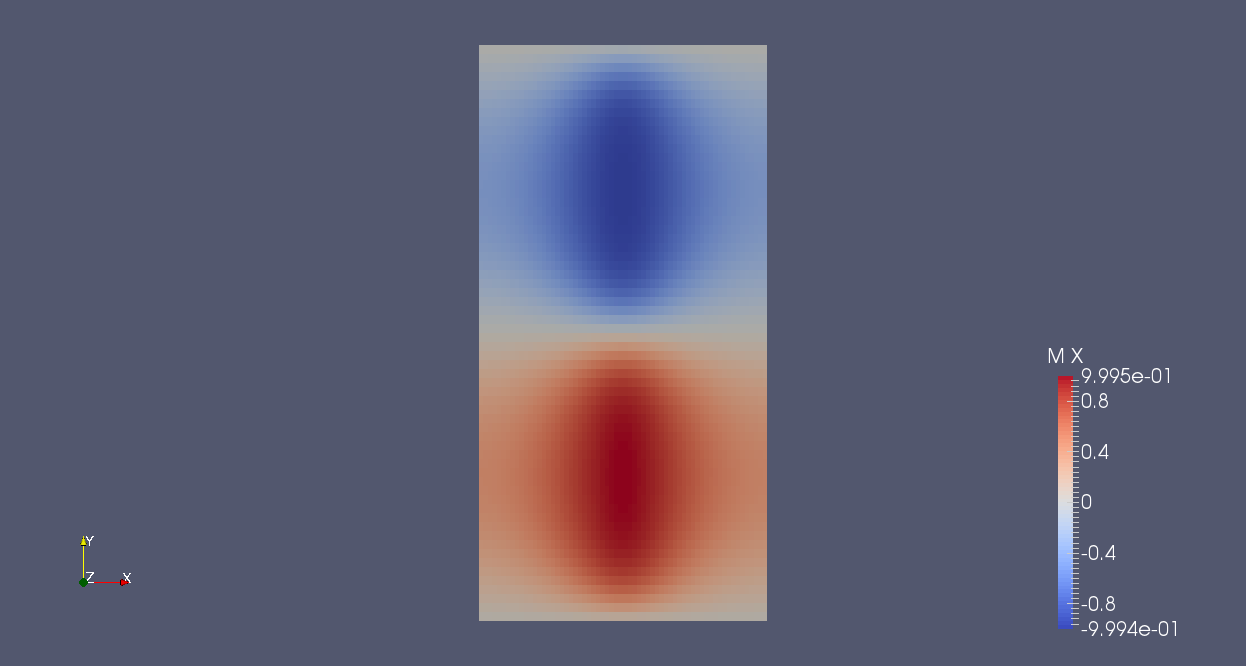
The initial magnetism M is oriented in the Y direction in half of the domain and in its opposite in the secund part.
| Parameter | description | 64x64x4 - Non Cubic | 64x128x8 - Non Cubic | 64x128x1 - Cubic | 256x512x4- Cubic |
| Ms | Aimantations (A/m) | 1.7e6 | - | - | - |
| K | Anisotropy (J/m^3) | 1.0e6 | - | - | - |
| A | Exchange (J/m^3) | 1.e-9 | - | - | - |
| Lex | exchange length (nm) \f$ \sqrt{\frac{2.A}{\mu.M_s^2}} \f$ | 23.47 | - | - | - |
| L | reference length (nm) | 3.125 | 1.5625 | 1.5625 | 0.391 |
| L/Lex | exchange influence | 0.133 | 0.067 | 0.067 | 0.017 |
The simulation parameters are:
| relaxation | taylor expansion |
| time | optimal |
| relaxation rate | 1.e-8 |
| toeplitz vector product | Tensorial |
 |
 |
| neighbors value | initial magnetism value along y |
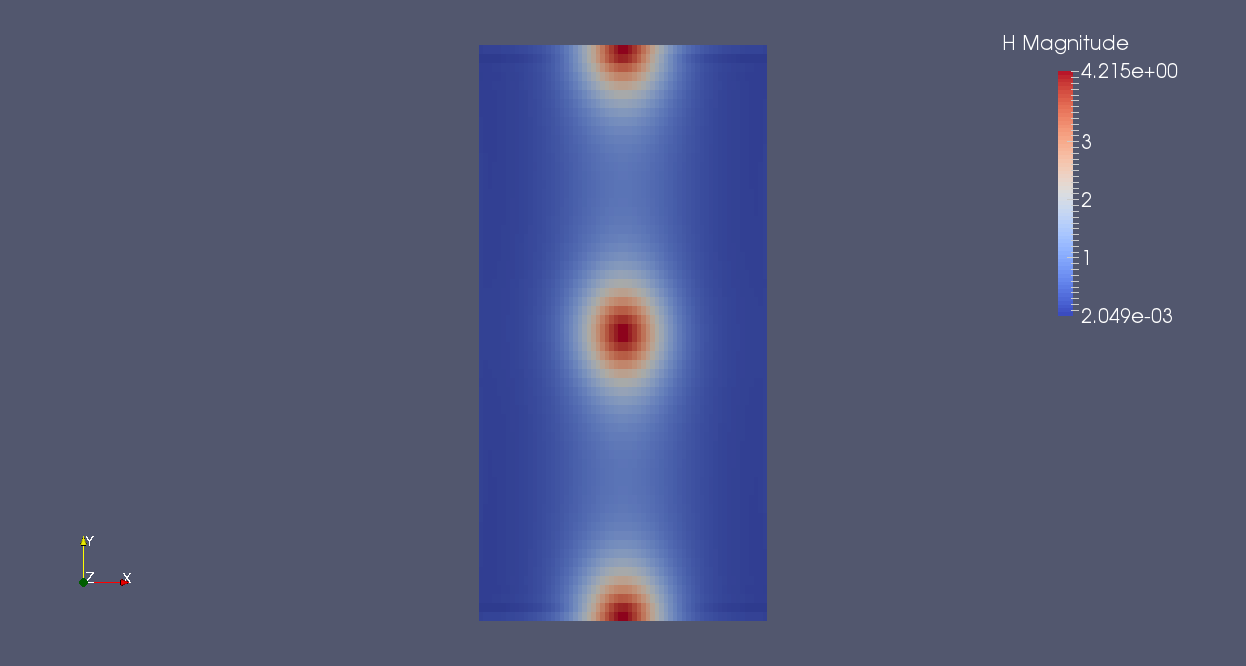
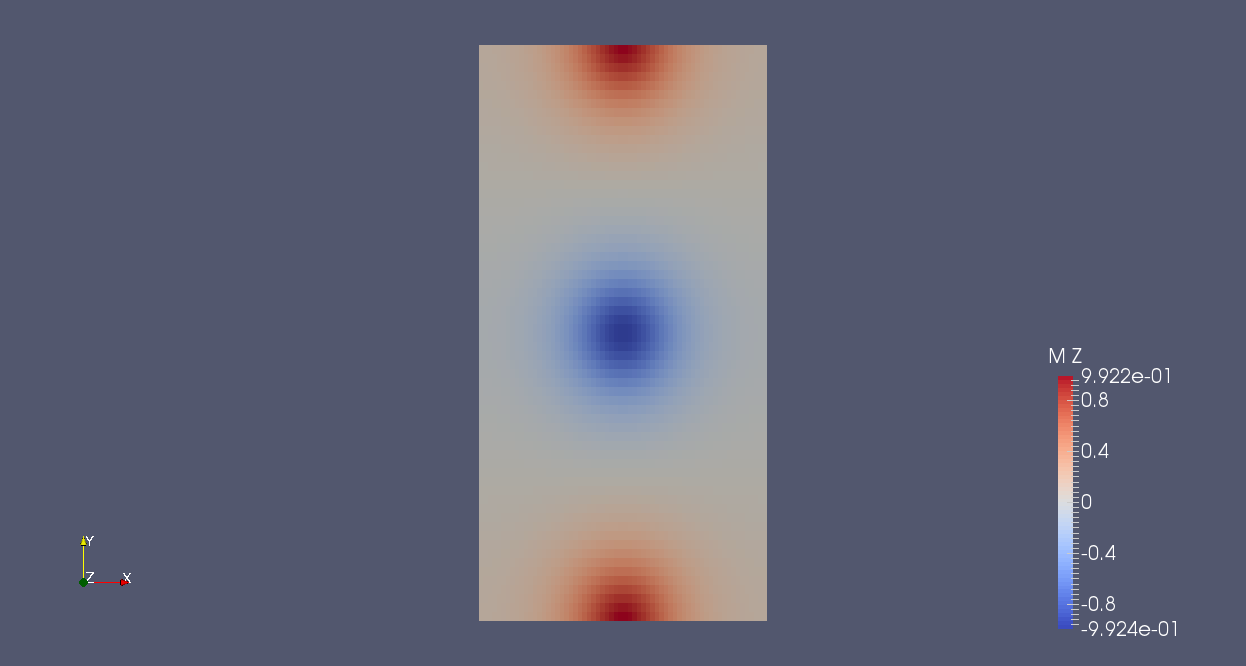
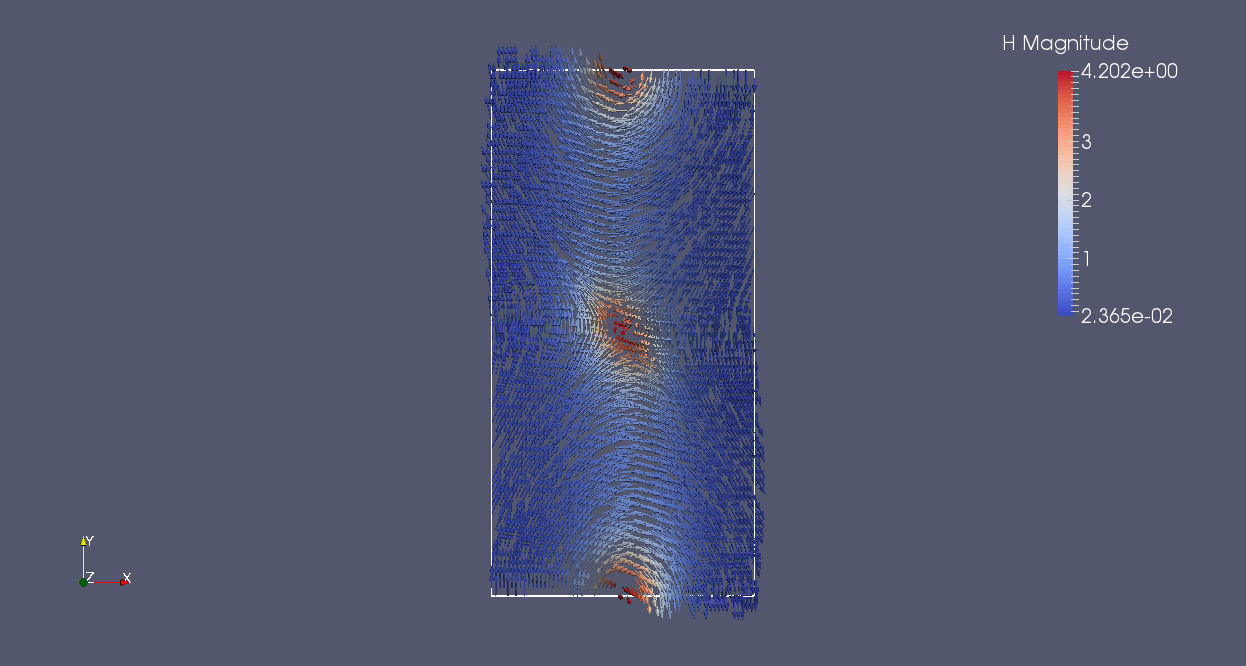
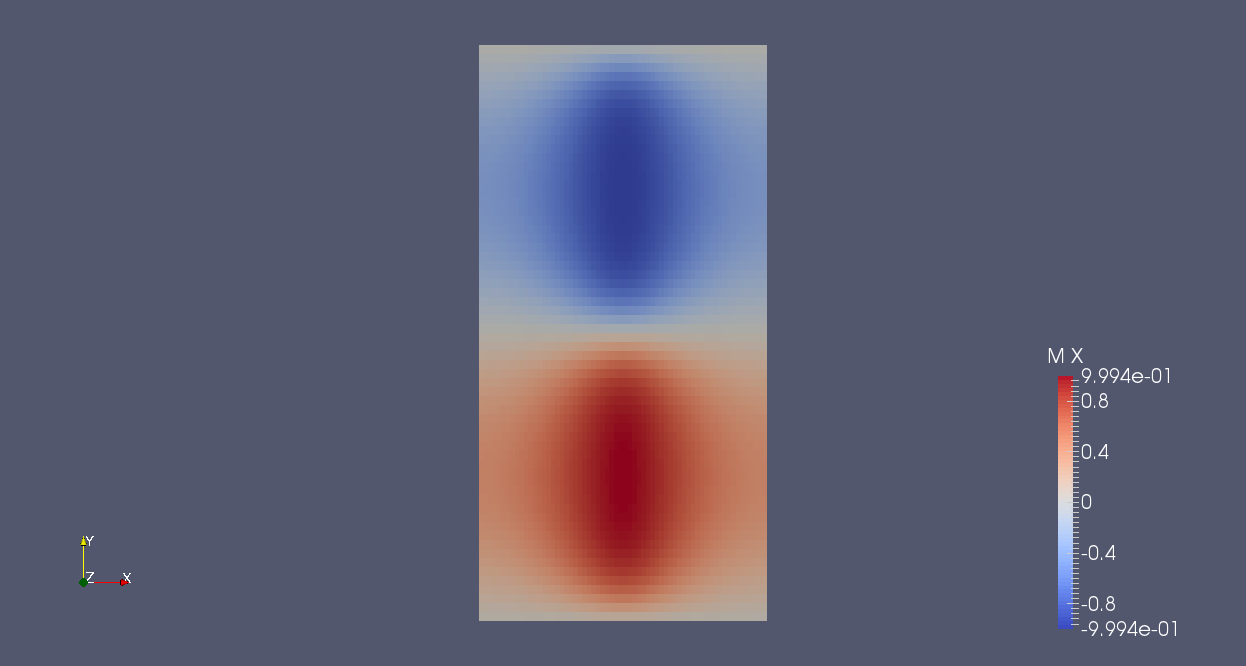
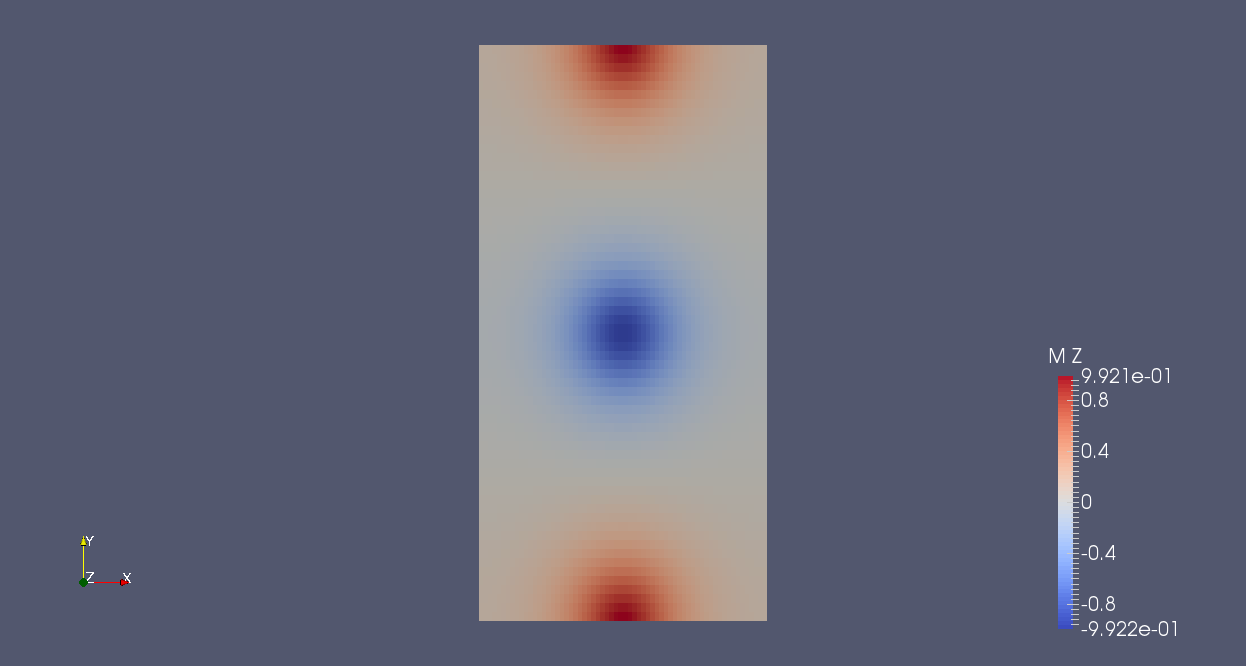
The compared results for non cubic cells for a thin sheet meshed by 64x64x4 elements for the CDG method and for the SDG method is given as follow:
 |
 |
 |
| equilibrium magnetism along x 64x64x4/CDG | equilibrium magnetism along y 64x64x4/CDG | equilibrium magnetism along z 64x64x4/CDG |
 |
 |
 |
| equilibrium magnetism, |H| colored in normal plane Ox 64x64x4/CDG | equilibrium magnetism, |H| colored in normal plane Oy 64x64x4/CDG | equilibrium magnetism, |H| colored in normal plane Oz 64x64x4/CDG |
 |
 |
 |
| equilibrium magnetism along x 64x64x4/SDG | equilibrium magnetism along y 64x64x4/SDG | equilibrium magnetism along z 64x64x4/SDG |
 |
 |
 |
| equilibrium magnetism, |H| colored in normal plane Ox 64x64x4/SDG | equilibrium magnetism, |H| colored in normal plane Oy 64x64x4/SDG | equilibrium magnetism, |H| colored in normal plane Oz 64x64x4/SDG |
 |
 |
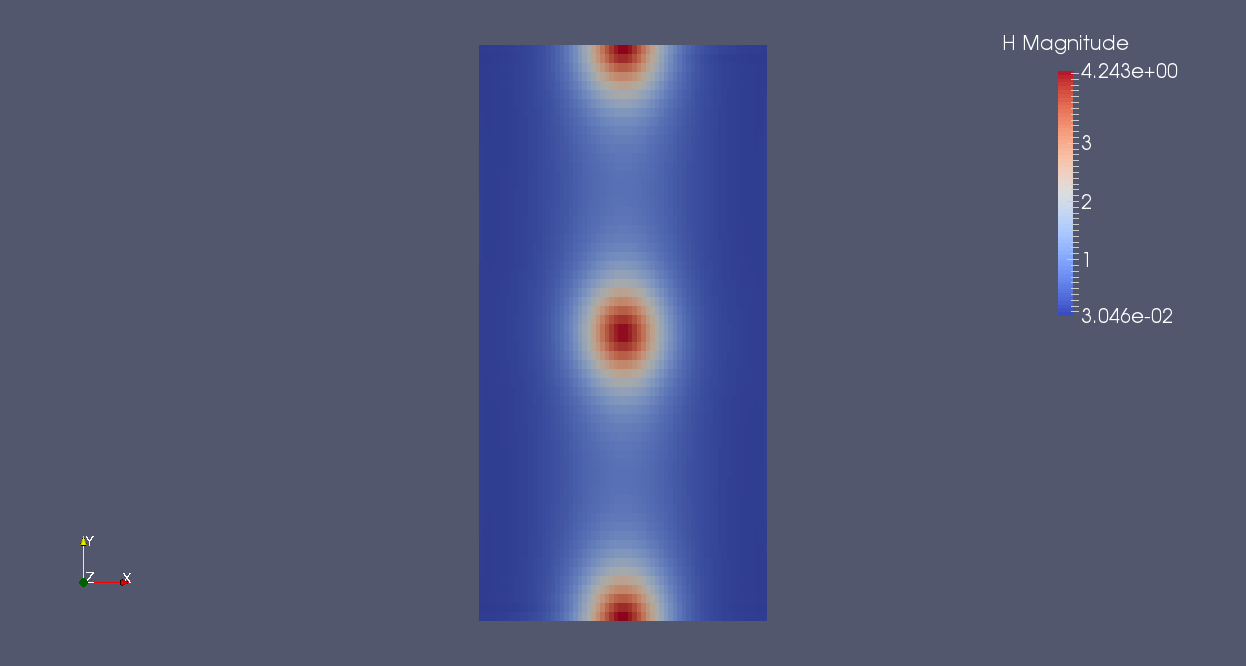| total magnetic excitation norm 64x64x4/CDG | total magnetic excitation norm 64x64x4/SDG |
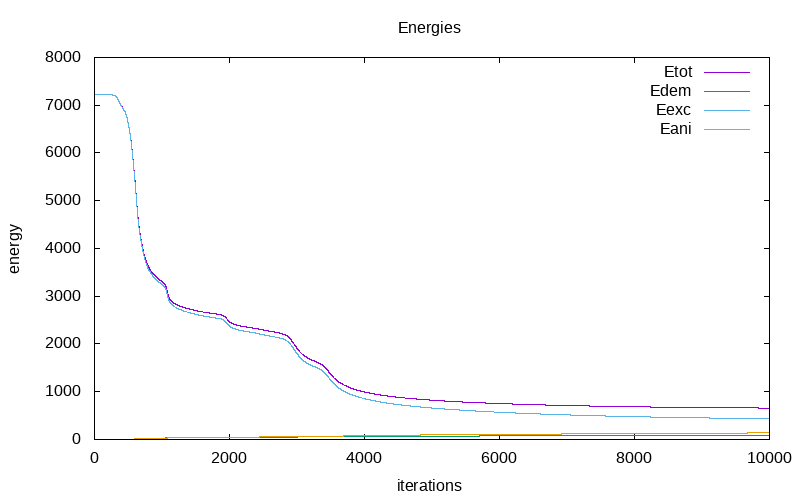
The evolution of energy during the relaxation process with respect of the iterations are as follow:
 |
 |
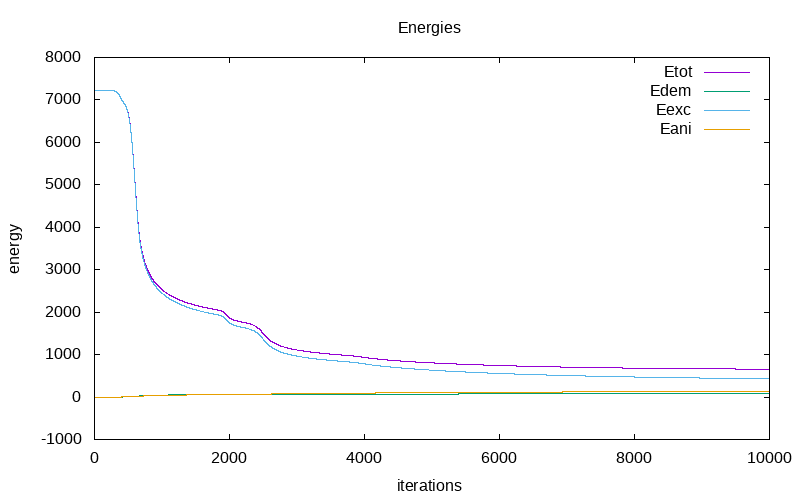| energy evolution on the non-cubic mesh 64x64x4/CDG | energy evolution on the non cubic mesh 64x64x4/SDG |
To validate the code, we compare the results with F77/C++ code with Toeplitz Matrix. Vector product based on 3-levels tensorial method and with SDG-RP method only valid for cubic cells.
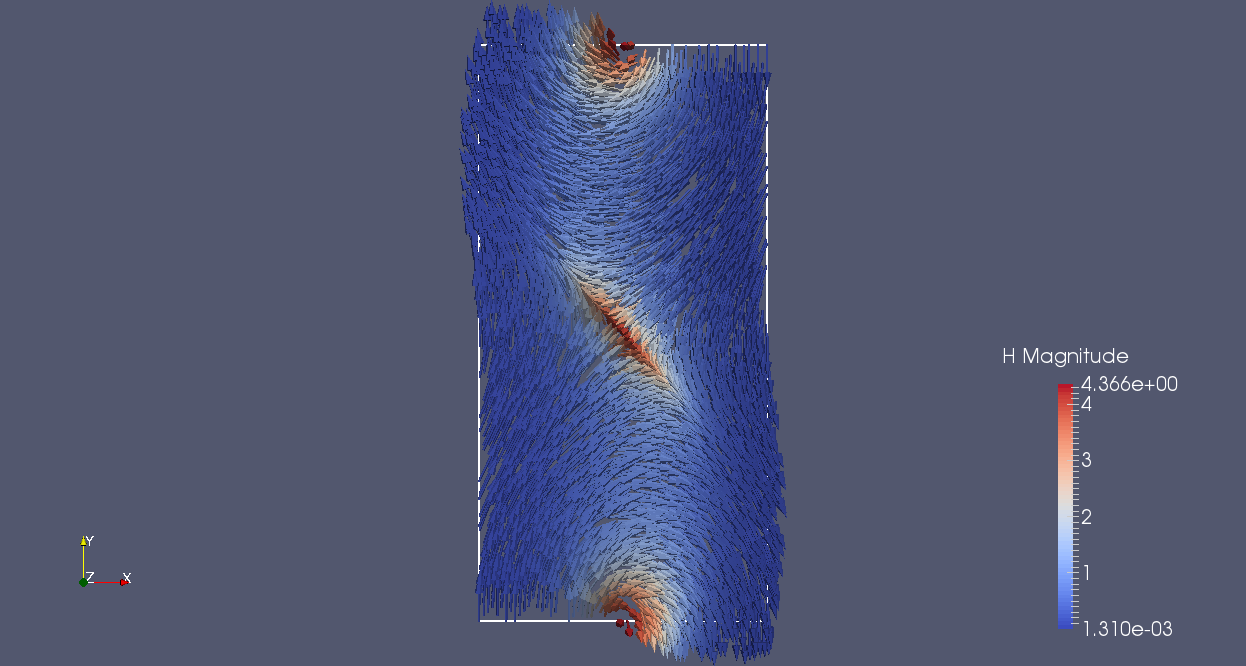
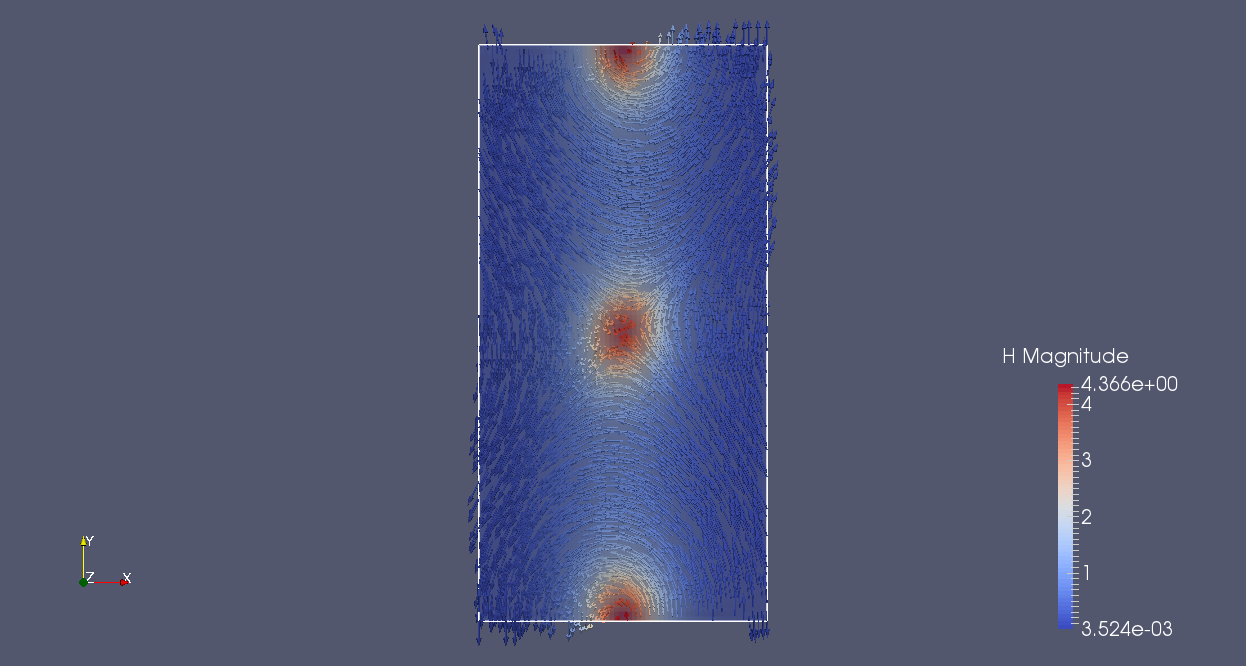
The compared results for cubic cells for a thin sheet meshed by 64x128x1 elements for the CDG method , for the SDG method and for the SDG-RP method are given as follow:
 |
 |
 |
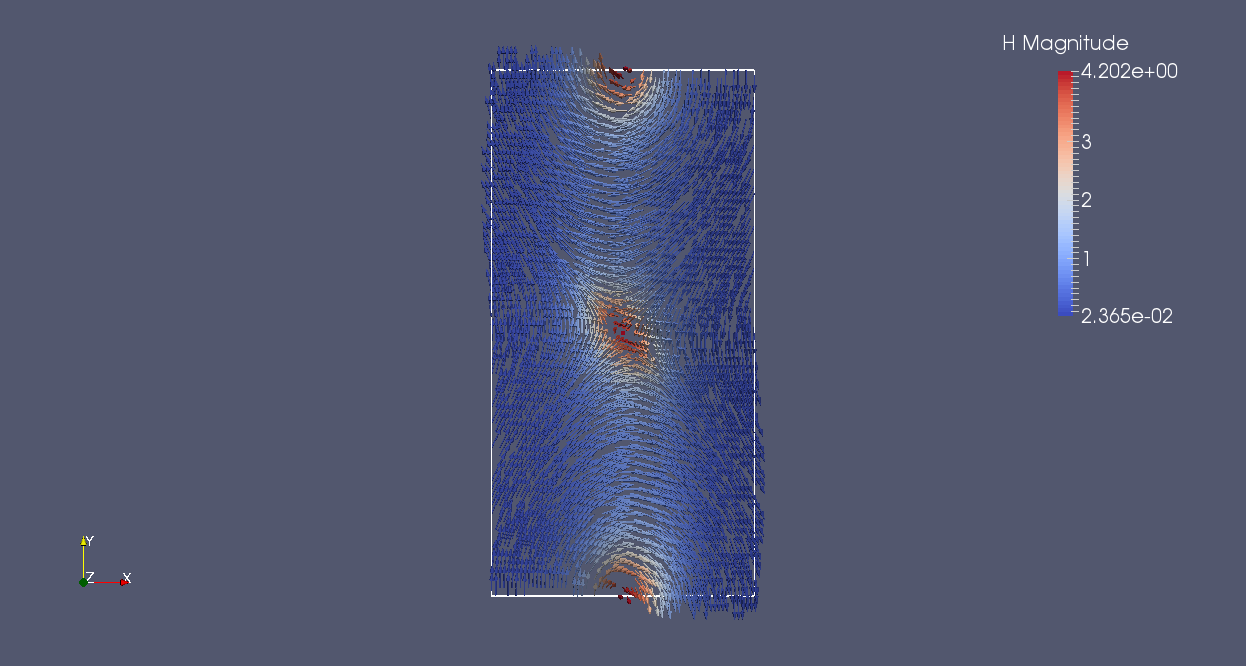
| equilibrium magnetism, |H| colored in normal plane Oz 64x128x1/CDG | equilibrium magnetism, |H| colored in normal plane Oz 64x128x1/SDG | equilibrium magnetism, |H| colored in normal plane Oz 64x128x1/SDG-RP |
 |
 |
 |
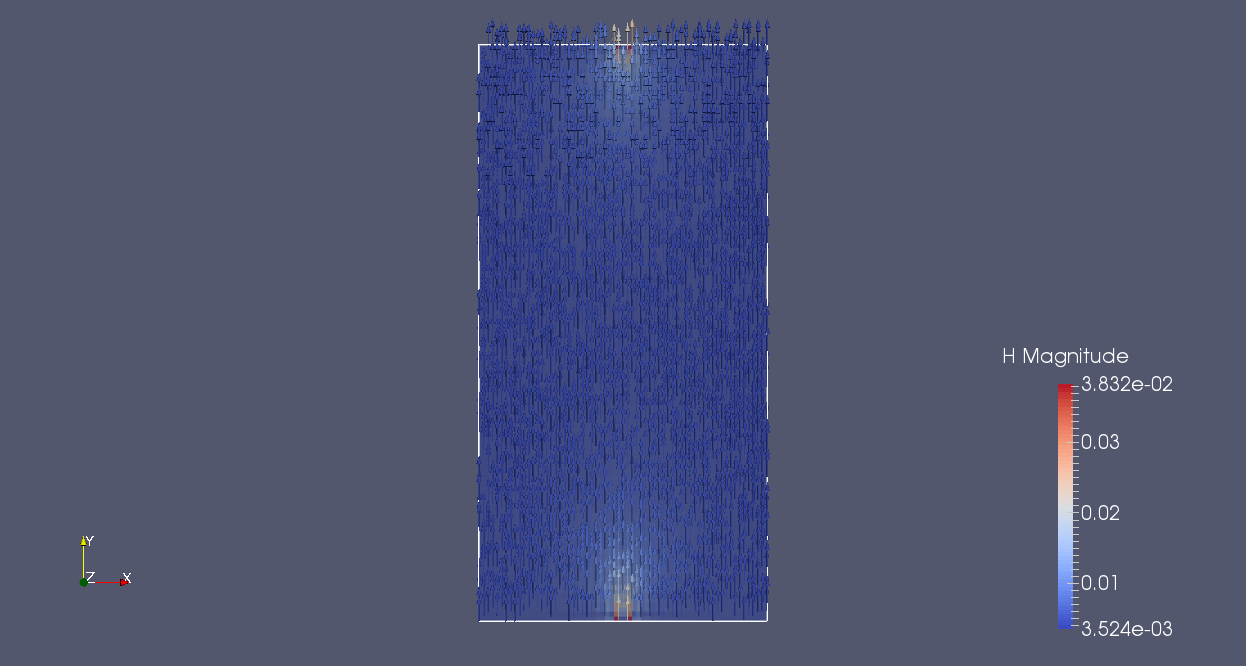| |H| CDG | |H| SDG | |H| SDG-RP |
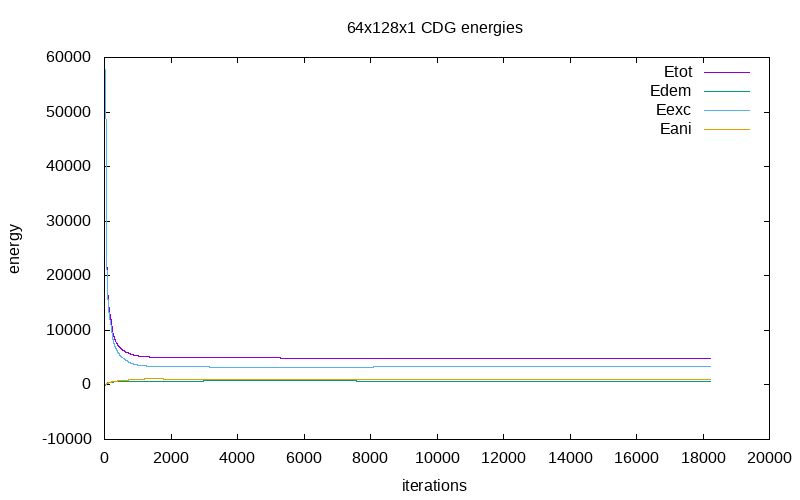
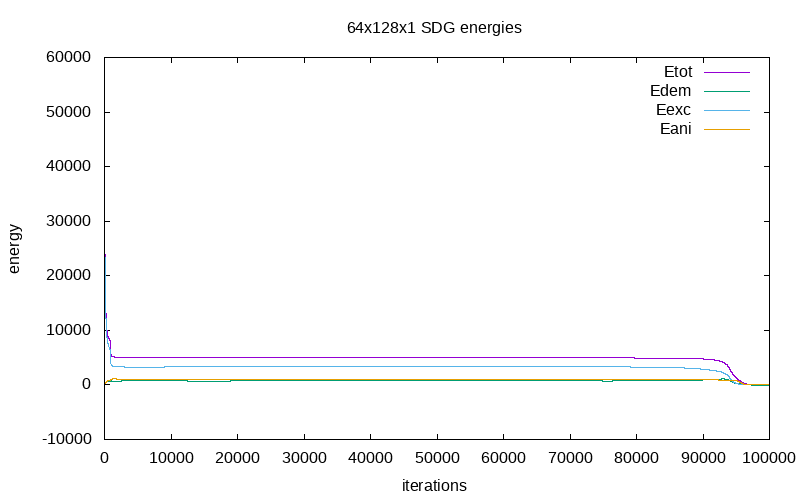
The evolution of energy during the relaxation process with respect of the iterations are as follow:
 |
 |
|
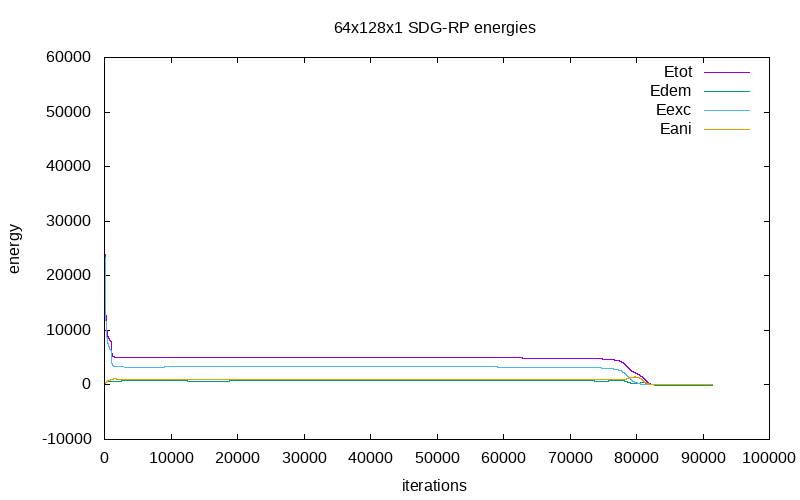| energy evolution on cubic mesh 64x128x1/CDG | energy evolution on cubic mesh 64x128x1/SDG | energy evolution on cubic mesh 64x128x1/SDG-RP |
We notice differents quilibrium states if the relaxation process is running long time enough (>75 000 iterations) depending on the accuracy of the methods used.
To reach the first equilibrium state, the relaxation criterium is eased to 1.e-7 (|DE/DT| < 1.e-7). We obtain the same results as the non cubic cells:
 |
 |
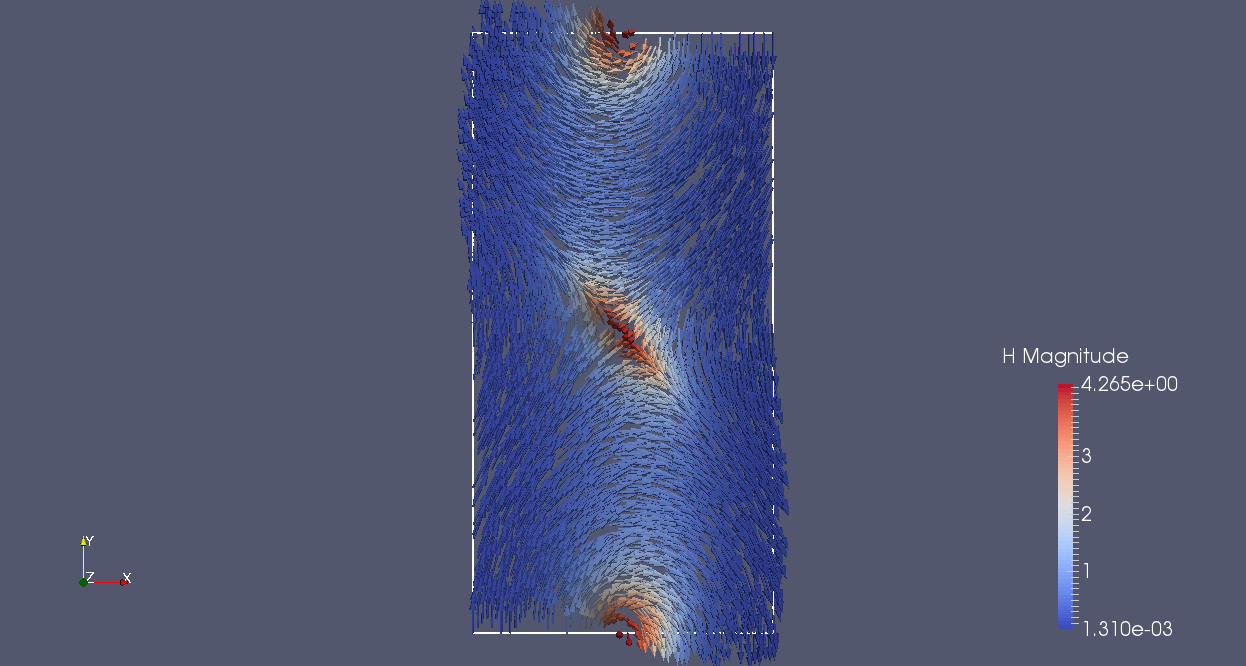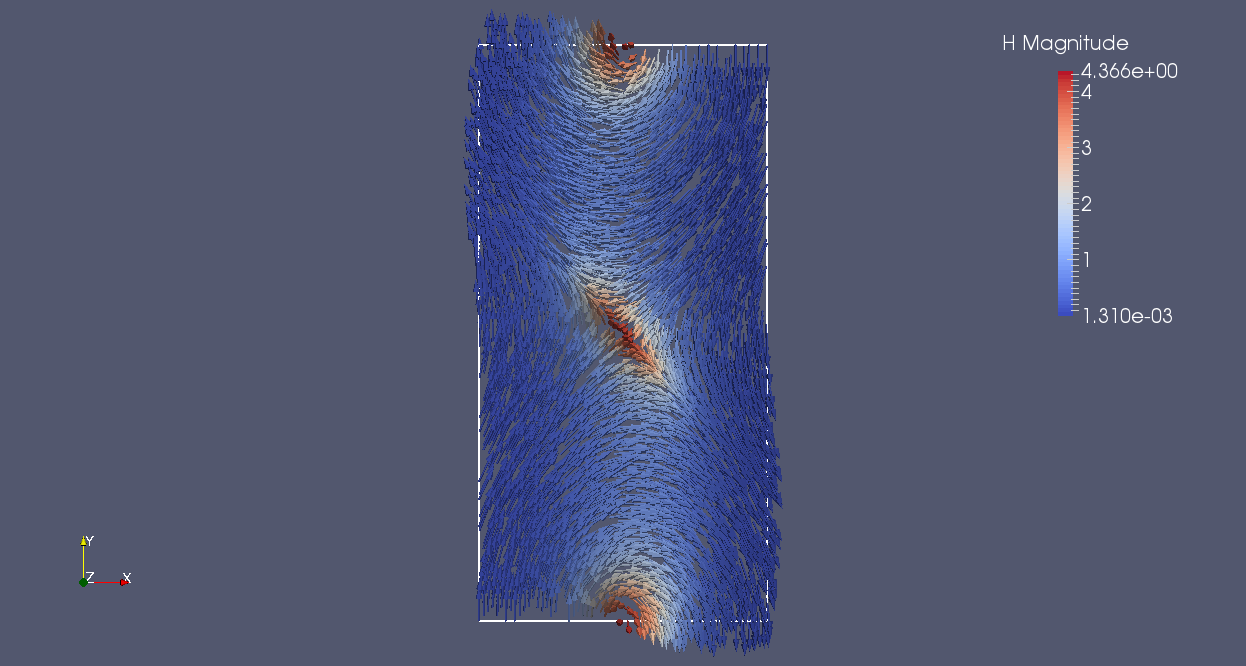| equilibrium magnetism, |H| colored in normal plane Oz 64x128x1 /SDG | equilibrium magnetism, |H| colored in normal plane Oz 64x128x1/SDG-RP |
 |
 |
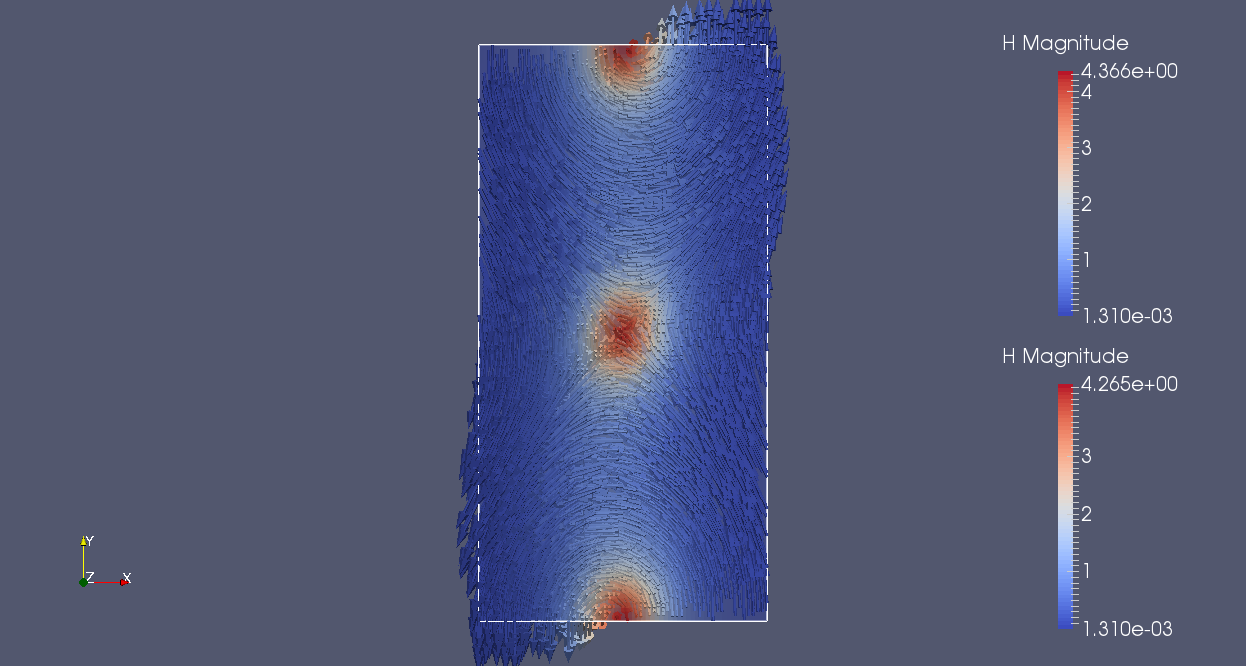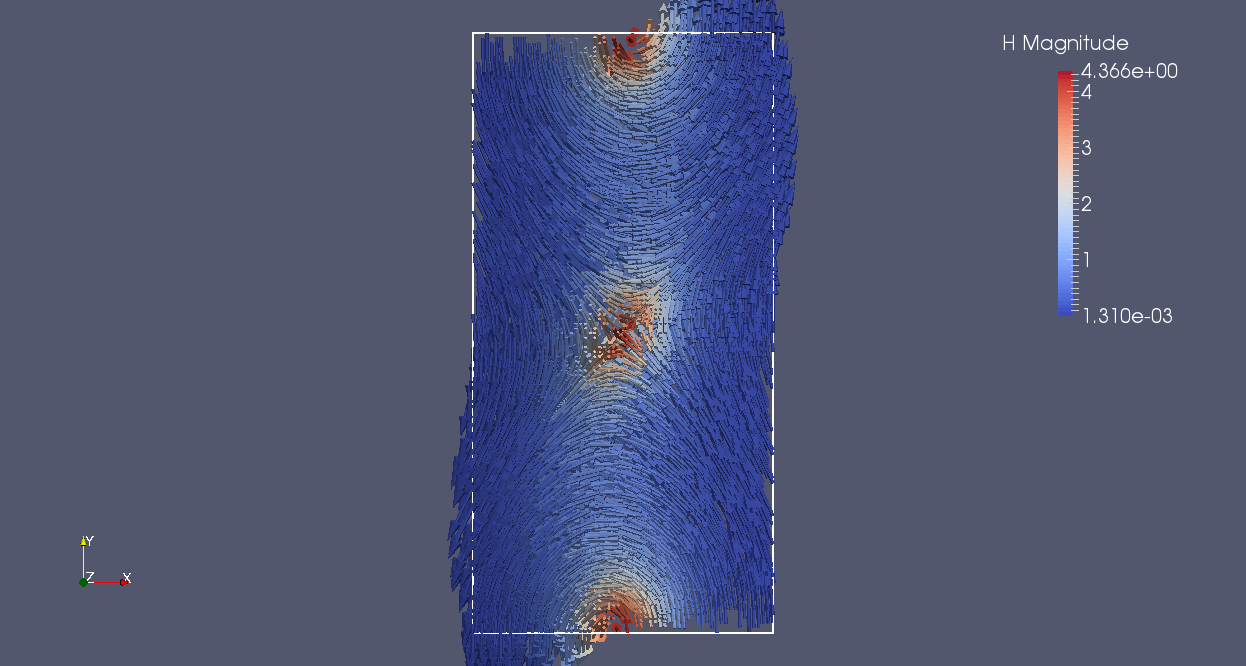| |H| SDG | |H| SDG-RP |
