The elastic bar is an paver of size 4x1x1 microns meshed by 64x16x16 cubic elements.
The matter parameters are as follow:
| Ms | Aimantations (A/m) | 1.7e6 |
| K | Anisotropy (J/m^3) | 1.e5 |
| A | Exchange (J/m^3) | 1.e-8 |
| rho | volumic mass(kg/m^3) | 7.83e3 |
| E | Young modulus(Pa) | 210e9 |
| nu | fish coefficient (no unit) | 0.3 |
| L100 | magnetostriction constant (no unit) | 21.e-6 |
| L111 | mmagnetostriction constant(no unit) | -21.e-6 |
The uniaxial anisotropy direction U1 is uniformly in the X-direction.
The initial magnetism M is uniformly in the direction (1,1,1).
There is no external magnetic excitation field.
The displacement is supposed to be a traction with null velocity.
The bar is fixed on the plane x=0 and free constraint anywhere else.
 |
| linear displacement U=(Ux,0,0) |
2 simulations are launched :
- one without magnetostriction
- oen with magnetostriction
the computation without magnetostriction converges in 700 iterations and stops because of the variation of energy is less than 1.e-8.
The value of of magnetism at equilibrium basic dyoptic grids are plot as follow:
 |
 |
 |
| equilibrium magnetism x-value | equilibrium magnetism y-value | equilibrium magnetism z-value |
 |
 |
 |
| total magnetic excitation H colored by |Hy| | norm of total magnetic excitation H | equilibrium magnetism M colored by |Mx| |
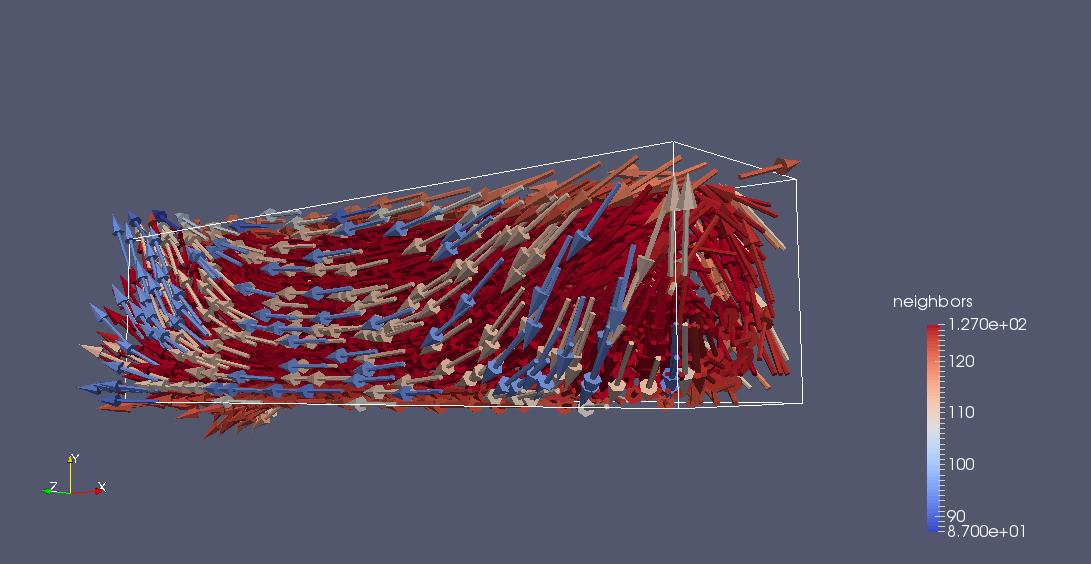
The value of of magnetism at equilibrium basic dyoptic grids are plot as follow:
 |
 |
 |
| equilibrium magnetism x-value | equilibrium magnetism y-value | equilibrium magnetism z-value |
 |
 |
 |
| total magnetic excitation H colored by N | norm of total magnetic excitation H | equilibrium magnetism M colored by |Mz| |
 |
| displacement field Ux at equilibrium |
The variation of energies during the first iterations are as follow: < td>
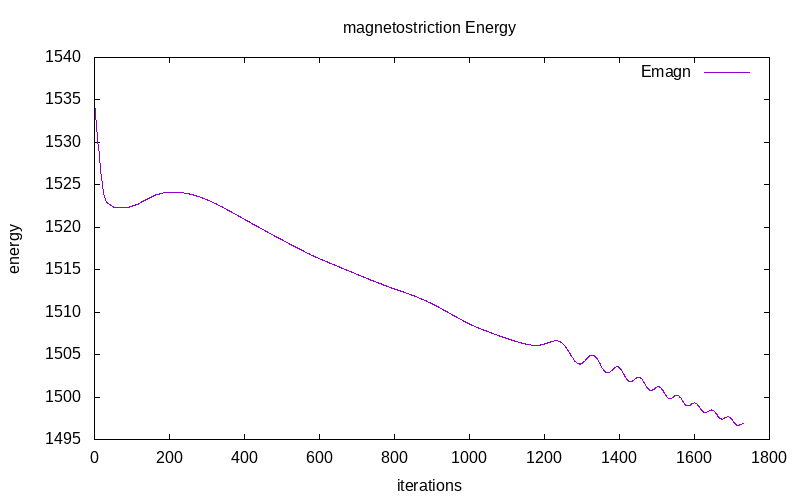
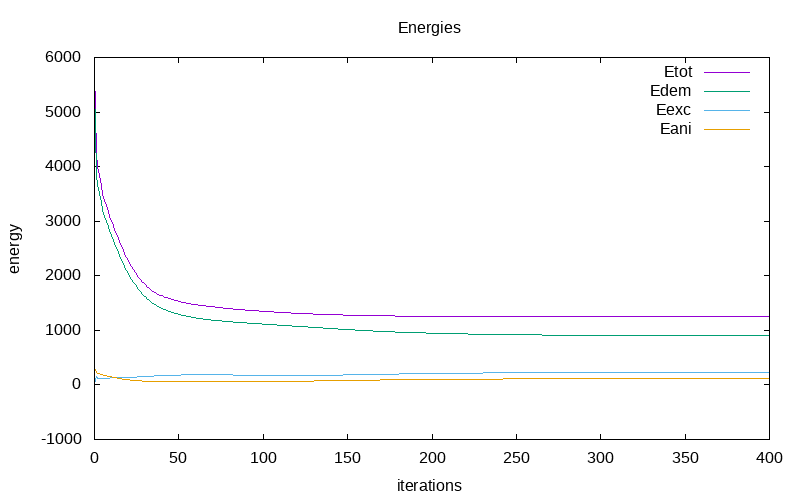 |
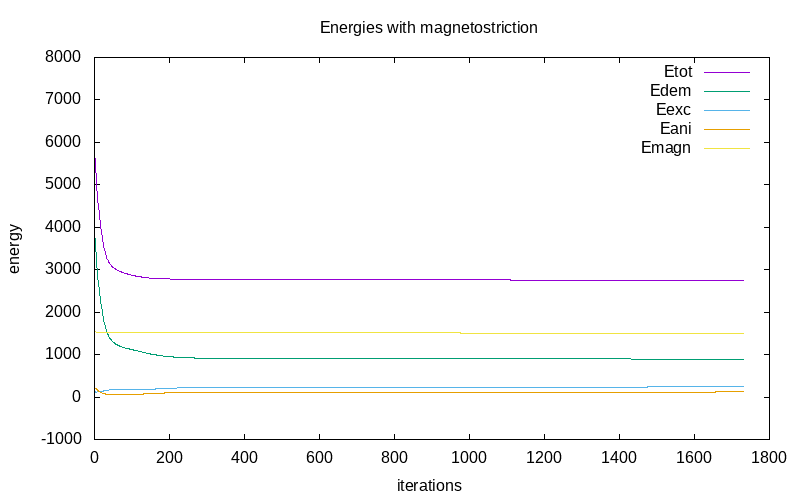 |
|
| All energies for without magnetostriction | all energies for with magnetistriction | magnetostriction Energy |
 1.8.13
1.8.13