The cross tie examples consists in studing a thin sheet of permalloy.

The sheet is rectangular with 0.64 micron of width, 1.28 micron of height & 0.01 micron of length.

The mesh constains 64 cells in X direction, 128 cells in Y direction & 1 cell in Z-direction.

mesh

Ms	Aimantations (A/m)	1.7e6
K	Anisotropy (J/m^3)	1.0e5
A	Exchange (J/m^3)	1.e-11
L	reference length (m)	1.e-8
L/Le	exchange influence	4.26

The anisotropy direction U1 is uniformly in the Y-direction with uniaxial crystal type The initial magnetism M is oriented in the Y direction in half of the domain and in its opposite in the secund part.


initial magnetism value along y	main anisotropy direction

The simulation parameters are:

relaxation	taylor expansion
time	optimal
relaxation rate	1.e-8
toeplitz vector product	LC
L/Le	exchange influence	4.26

The the results are as follow:

The value of magnetism field at equilibrium state are plot as follow:


equilibrium magnetism value along x	equilibrium magnetism value along y	equilibrium magnetism value along z


equilibrium magnetism vector with total magnetism module	equilibrium total magnetic excitation field norm

In order to vizualize the effect of the diffusion process we have to change the matter data to respect the relation 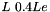$ L~0.4 Le $ : The matter parameters are as follow:

Ms	Aimantations (A/m)	1.7e6
K	Anisotropy (J/m^3)	1.0e5
A	Exchange (J/m^3)	1.e-9
L	reference length (m)	1.e-8
L/Le	exchange influence	1

The configurations is as follow:

The value of magnetism field at equilibrium state are plot as follow:


equilibrium magnetism vector with total magnetism module<	equilibrium total magnetism field norm


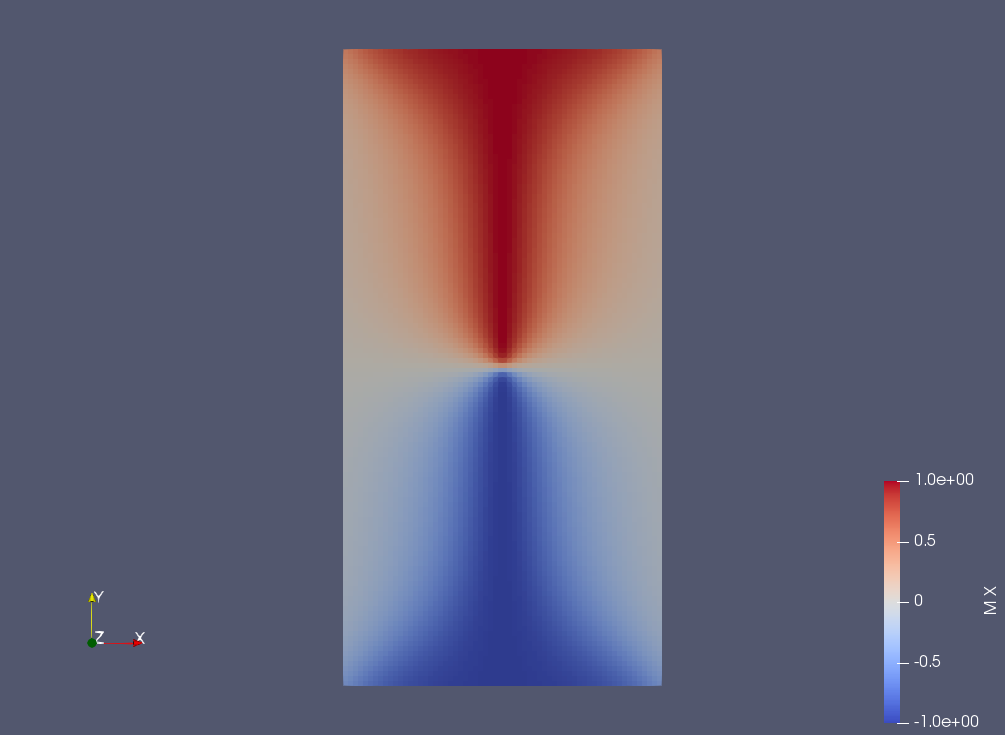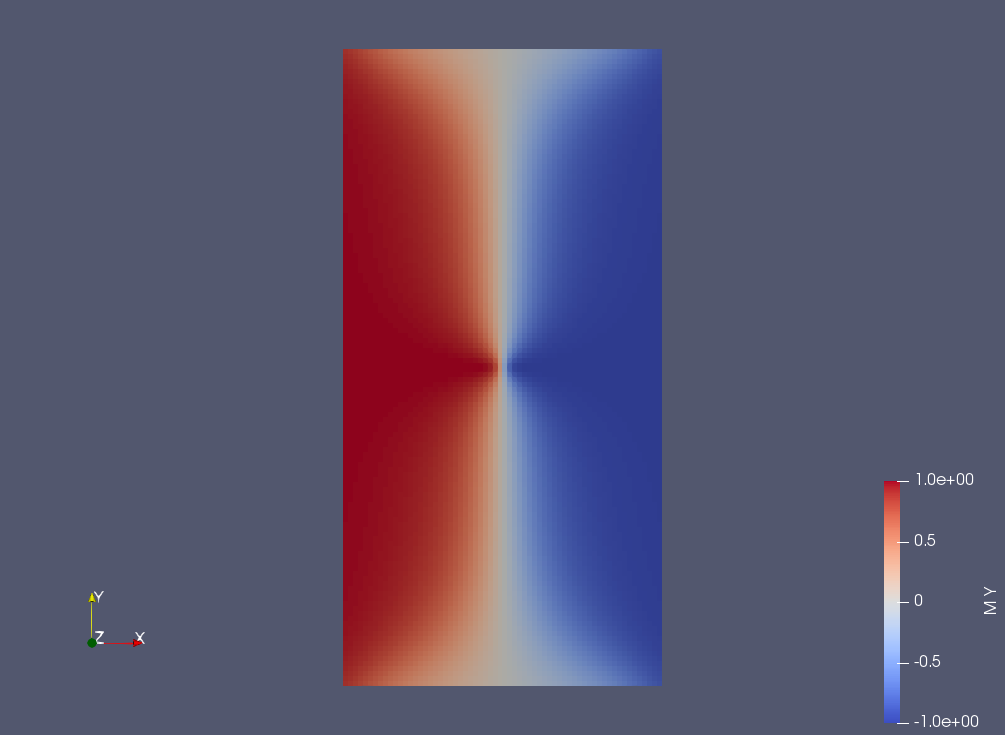equilibrium magnetism vector along X at iter 723	equilibrium magnetism vector along Y at iter 723	equilibrium magnetism vector along Z at iter 723

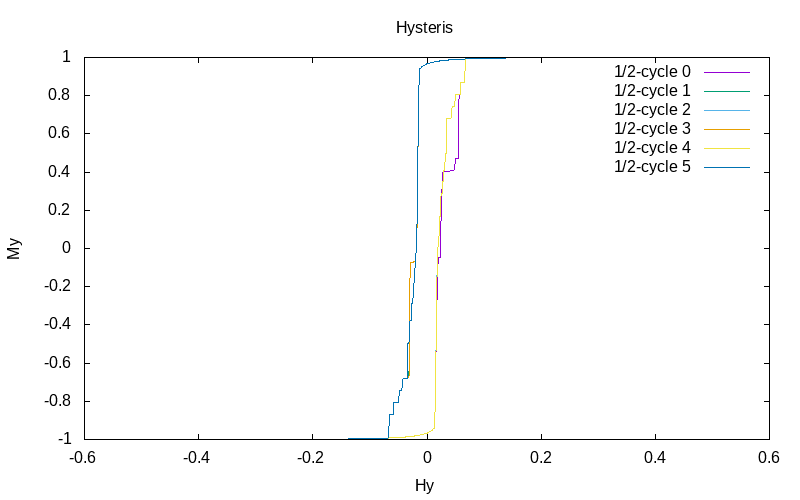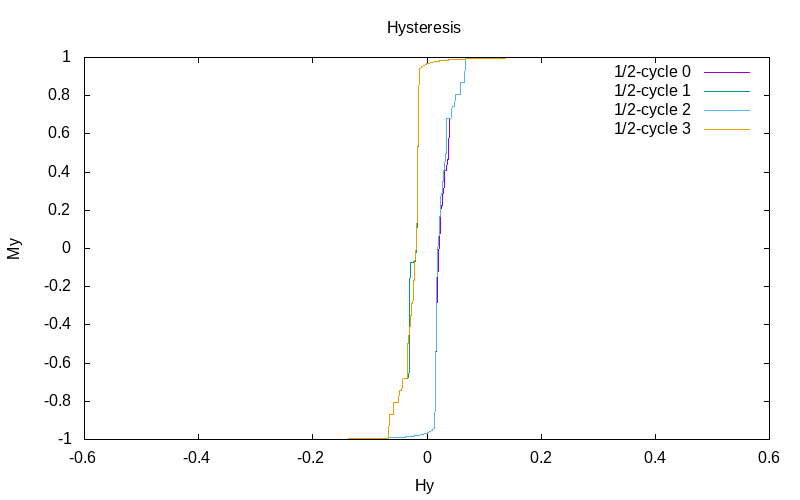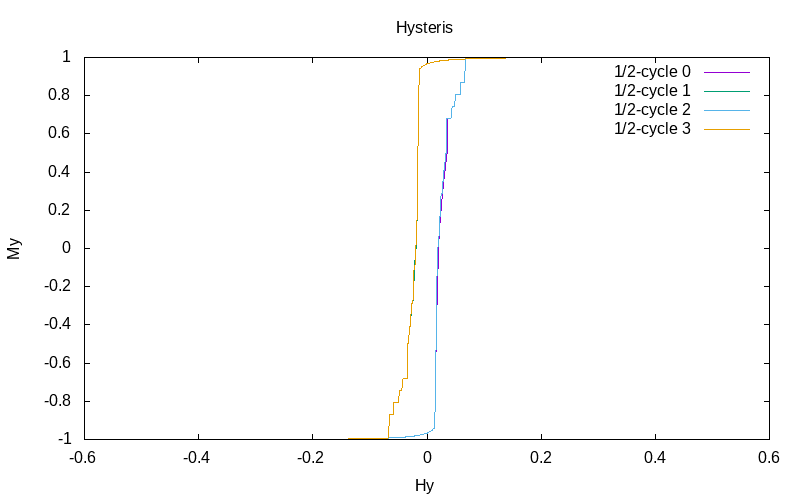Hysteresis cycles are also computed with Hext varying form [0,-0.5,0] to [0,0.5,0] from increment of 0.001 for A=1.e-9 with several implementations of toeplitz . vector product: <


3 hysteresis cycles for elementary circular product	3 hysteresis cycles for elementary tensor product	3 hysteresis cycles for RP implementation of elementary tensor product

PS: to show the field of M apply the filters to field M:

cellDatatoPointData
glyph choose vectors to M and select magnitude of H in the viewer