Multi-frequency averaging and uniform accuracy towards numerical approximations for a Bloch model
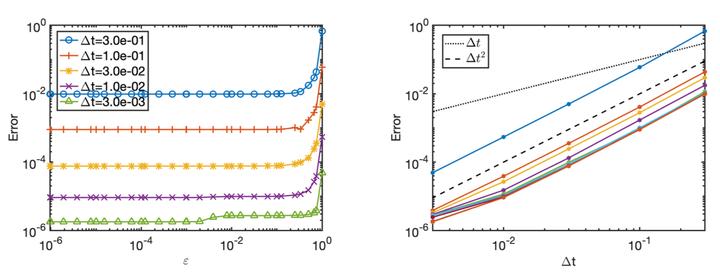 Error for the Bloch model using a second order UA scheme
Error for the Bloch model using a second order UA scheme
Abstract
We are interested in numerically solving a transitional model derived from the Bloch model. The Bloch equation describes the time evolution of the density matrix of a quantum system forced by an electromagnetic wave. In a high frequency and low amplitude regime, it asymptotically reduces to a non-stiff rate equation. As a middle ground, the transitional model governs the diagonal part of the density matrix. It fits in a general setting of linear problems with a high-frequency quasi-periodic forcing and an exponentially decaying forcing. The numerical resolution of such problems is challenging. Adapting high-order averaging techniques to this setting, we separate the slow (rate) dynamics from the fast (oscillatory and decay) dynamics to derive a new micro-macro problem. We derive estimates for the size of the micro part of the decomposition, and of its time derivatives, showing that this new problem is non-stiff. As such, we may solve this micro-macro problem with uniform accuracy using standard numerical schemes. To validate this approach, we present numerical results first on a toy problem and then on the transitional Bloch model.