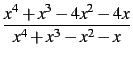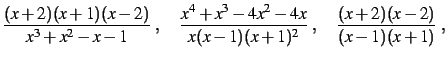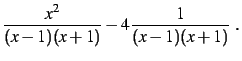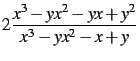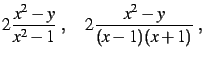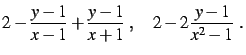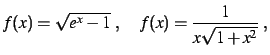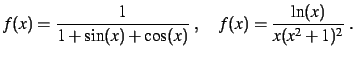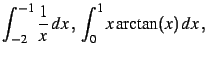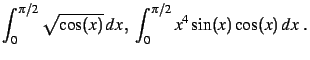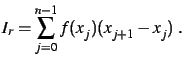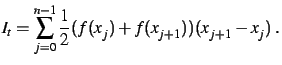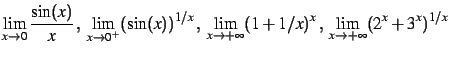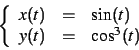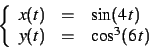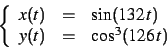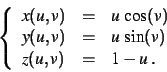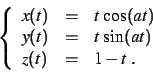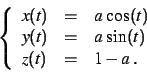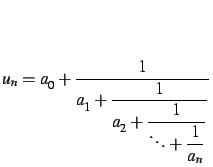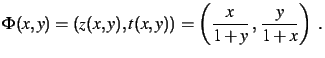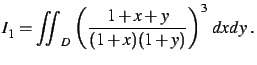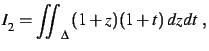Section : dxcas
Avant :
Vrai ou Faux ?
Après : Index
Il y a souvent plusieurs manières d'obtenir le même résultat en
Xcas. On s'efforcera de choisir les solutions les plus compactes.
Corrigé exercice 8.1
Exercice 8.2
Transformer la fraction rationnelle
en les fractions suivantes
Corrigé exercice 8.2
Exercice 8.3
Transformer la fraction rationnelle
en les fractions suivantes
Corrigé exercice 8.3
Exercice 8.4
On considère les fonctions
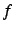
définies par
Pour chacune de ces fonctions :
- Calculer une primitive
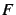 .
.
- Calculer
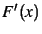 et montrer que
et montrer que
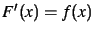 après simplifications.
après simplifications.
Corrigé exercice 8.4
Exercice 8.5
On considère les intégrales définies
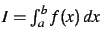
suivantes.
Pour chacune de ces intégrales :
- Calculer la valeur exacte, puis approchée de l'intégrale
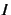 .
.
- Pour
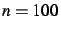 , puis
, puis 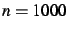 , et
pour tout
, et
pour tout
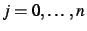 , on pose
, on pose
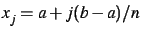 , et
, et
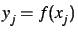 .
Calculer la valeur approchée de l'intégrale
.
Calculer la valeur approchée de l'intégrale 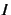 par la
méthode des rectangles à gauche :
par la
méthode des rectangles à gauche :
- Même question avec la méthode des trapèzes :
Corrigé exercice 8.5
Corrigé exercice 8.6
Corrigé exercice 8.7
Exercice 8.8
On considère les limites suivantes.
Pour chacune d'entre elles :
- Donner sa valeur exacte.
- Trouver une valeur de
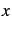 telle que la distance de
telle que la distance de 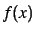 à la
limite soit inférieure à
à la
limite soit inférieure à 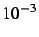 .
.
Corrigé exercice 8.8
Corrigé exercice 8.9
Corrigé exercice 8.10
Exercice 8.11
- Représenter la fonction
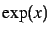 sur l'intervalle
sur l'intervalle ![$ [-1,1]$](img136.gif) .
Sur ce graphique, tracer aussi les représentations
des polynômes de Taylor de cette fonction en
.
Sur ce graphique, tracer aussi les représentations
des polynômes de Taylor de cette fonction en 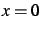 , aux ordres
, aux ordres
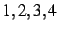 .
.
- Même question pour l'intervalle
![$ [1,2]$](img139.gif) .
.
- Représenter la fonction
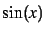 sur l'intervalle
sur l'intervalle
![$ [-\pi,\pi]$](img141.gif) . Sur
le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en
. Sur
le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en 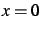 , aux ordres
, aux ordres
 .
.
Corrigé exercice 8.11
Corrigé exercice 8.12
Corrigé exercice 8.13
Exercice 8.14
Pour chacune des courbes paramétrées suivantes, on choisira un
intervalle de valeurs du paramètre
assurant une représentation complète et suffisamment lisse.
-
-
-
Corrigé exercice 8.14
Corrigé exercice 8.15
Exercice 8.16
Le but de l'exercice est de visualiser un cône de différentes
manières.
- Représenter la surface d'équation
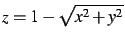 .
.
- Représenter la surface paramétrée définie par :
- En choisisant une valeur de
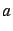 suffisamment grande, représenter la courbe
paramétrée définie par :
suffisamment grande, représenter la courbe
paramétrée définie par :
- Représenter la famille de courbes paramétrées définies par :
- Représenter le même cône en utilisant la fonction
cone.
Corrigé exercice 8.16
Exercice 8.17
- Engendrer une liste
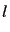 de
de 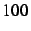 entiers au hasard entre
entiers au hasard entre 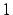 et
et 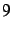 .
.
- Vérifier que l'ensemble des valeurs de
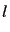 est contenu dans
est contenu dans
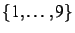 .
.
- Extraire de la liste
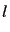 toutes les valeurs
toutes les valeurs 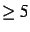 .
.
- Pour tout
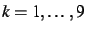 , compter combien de valeurs de la liste
, compter combien de valeurs de la liste 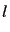 sont égales à
sont égales à 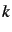 .
.
Corrigé exercice 8.17
Exercice 8.18
Si
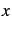
est un réel, la fraction continue à l'ordre
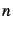
de
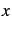
est
une liste
![$ [a_0,\ldots,a_n]$](img168.gif)
d'entiers, dont le premier terme
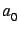
est la partie entière de
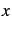
. Pour tout
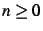
,
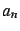
est la
partie entière de l'inverse de la partie décimale de
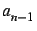
.
La liste
![$ [a_0,\ldots,a_n]$](img168.gif)
est associée au rationnel
Pour
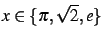
et
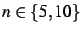
:
- Calculer
![$ [a_0,\ldots,a_n]$](img168.gif) .
.
- Comparer votre résultat avec celui que donne la fonction
dfc
de Xcas.
- Calculer
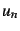 , et donner la valeur numérique de
, et donner la valeur numérique de 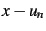 .
.
Corrigé exercice 8.18
Exercice 8.19
Ecrire (sans utiliser de boucle) les séquences suivantes :
- Nombres de
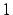 à
à 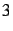 par pas de
par pas de 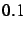 .
.
- Nombres de
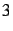 à
à 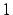 par pas de
par pas de 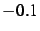 .
.
- Carrés des
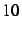 premiers entiers.
premiers entiers.
- Nombres de la forme
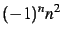 pour
pour
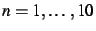 .
.
- 10 "0" suivis de 10 "1".
- 3 "0" suivis de 3 "1", suivis de 3 "2",...,
suivis de 3 "9".
- "1", suivi de 1 "0", suivi de "2", suivi de 2 "0",...
, suivi de "8", suivi de 8 zéros, suivi de "9".
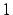 "
"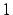 " suivi de
" suivi de 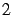 "
"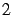 ", suivis de
", suivis de 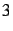 "
"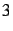 ",...,
suivis de
",...,
suivis de 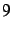 "
"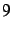 ".
".
Corrigé exercice 8.19
Corrigé exercice 8.20
Exercice 8.21
- Ecrire la matrice carrée
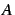 d'ordre
d'ordre 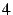 , telle que
, telle que 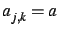 si
si 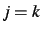 et
et
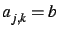 si
si 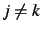 , où
, où 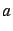 et
et 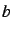 sont des variables.
sont des variables.
- Calculer et factoriser le polynôme caractéristique de
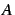 .
.
- Déterminer une matrice orthogonale
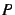 telle que
telle que
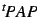 soit
une matrice diagonale.
soit
une matrice diagonale.
- Utiliser la question précédente pour définir la fonction
qui à un entier
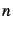 associe la matrice
associe la matrice 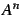 .
.
- Calculer
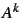 , pour
, pour
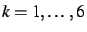 en effectuant les produits
matriciels, et vérifier que la fonction définie à la question
précédente donne bien le même résultat.
en effectuant les produits
matriciels, et vérifier que la fonction définie à la question
précédente donne bien le même résultat.
Corrigé exercice 8.21
Corrigé exercice 8.22
Corrigé exercice 8.23
Exercice 8.24
Ecrire les fonctions suivantes. Toutes prennent en entrée une fonction
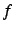
(de
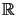
dans
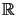
), et trois valeurs
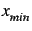
,
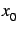
et
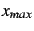
(supposées telles que
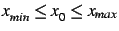
).
derive :
Elle calcule et représente graphiquement
la dérivée de 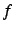 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img227.gif) . Elle retourne la
une valeur de
. Elle retourne la
une valeur de 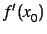 .
.tangente :
Elle représente la fonction 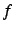 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img227.gif) , elle
superpose sur le même graphique la tangente à
, elle
superpose sur le même graphique la tangente à 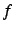 au point
au point 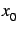 , et
retourne l'équation de cette tangente comme un polynôme du premier
degré.
, et
retourne l'équation de cette tangente comme un polynôme du premier
degré.araignee :
Elle représente la fonction 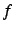 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img227.gif) ,
ainsi que la droite d'équation
,
ainsi que la droite d'équation 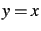 (première bissectrice).
Elle calcule et retourne les
(première bissectrice).
Elle calcule et retourne les 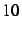 premiers itérés de
premiers itérés de 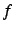 en
en 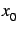 (
(
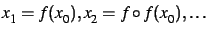 ). Elle représente la suite de
segments, alternativement verticaux et horizontaux, permettant de visualiser
les itérations : segments joignant
). Elle représente la suite de
segments, alternativement verticaux et horizontaux, permettant de visualiser
les itérations : segments joignant 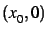 ,
, 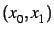 ,
, 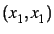 ,
,
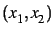 ,
, 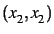 , ...
(comparer avec la fonction
, ...
(comparer avec la fonction plotseq)newton_graph :
Elle représente la fonction 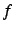 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img227.gif) .
Elle calcule et retourne les dix premiers itérés de la suite définie
à partir de
.
Elle calcule et retourne les dix premiers itérés de la suite définie
à partir de 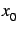 par la méthode de Newton :
par la méthode de Newton :
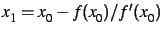 ,
,
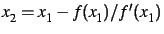 ... Les valeurs de la dérivée sont
approchées. La fonction représente sur le même graphique les
segments permettant de visualiser les itérations : segments joignant
... Les valeurs de la dérivée sont
approchées. La fonction représente sur le même graphique les
segments permettant de visualiser les itérations : segments joignant
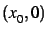 ,
,
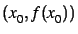 ,
, 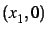 ,
,
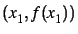 ,
, 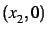 ,
,
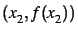 ,...
(comparer avec la fonction
,...
(comparer avec la fonction newton)
Corrigé exercice 8.24
Corrigé exercice 8.25
Section : dxcas
Avant : Vrai ou Faux ?
Après : Index
R. De Graeve, B. Parisse, B. Ycart 2006