Section : dxcas
Avant : Style de programmation
Après : Exercices

Vrai ou Faux ?

Exercice 7.1   Les commandes suivantes affichent la valeur exacte 2 : vrai ou faux et pourquoi ?

1. $\square\;$ 1+1:;
2. $\boxtimes\;$ 3-1
3. $\square\;$ 1.5+1/2
4. $\boxtimes\;$ 4/2
5. $\boxtimes\;$ sqrt(4)
6. $\square\;$ evalf(sqrt(4))
7. $\boxtimes\;$ 1^(1+1)+1^(1+1)
8. $\square\;$ (1+1)^(1+1)
9. $\square\;$ 1*1^(1+1)
10. $\boxtimes\;$ 1+1*1^1
11. $\boxtimes\;$ (1+1)*1^(1+1)
12. $\square\;$ 1^2/-1
13. $\boxtimes\;$ 1/2^-1

Exercice 7.2   Les commandes suivantes affectent la valeur exacte 2 à la variable c : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ c:=2:;
2. $\boxtimes\;$ c:=2
3. $\square\;$ c==2
4. $\square\;$ c=2
5. $\boxtimes\;$ c:=4/2
6. $\square\;$ c:=3/1.5
7. $\boxtimes\;$ c:=(2+2)/2
8. $\square\;$ c:=(2.0+2)/2
9. $\square\;$ c:=2a/a
10. $\square\;$ c:=(2*a)/a
11. $\boxtimes\;$ c:=2*a/a
12. $\boxtimes\;$ c:=1:; c:=2*c

Exercice 7.3   Les commandes suivantes affectent à la variable c une expression valide : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ c:=ab
2. $\boxtimes\;$ c:=a*b
3. $\square\;$ c==a
4. $\boxtimes\;$ c:= c==a
5. $\square\;$ c:=a+(a*b))/2
6. $\square\;$ c=a+a*b
7. $\boxtimes\;$ c:=a/b
8. $\square\;$ c->a/b
9. $\boxtimes\;$ a/b=>c
10. $\boxtimes\;$ c:=a/0
11. $\boxtimes\;$ c:=2*a/a
12. $\square\;$ c:=1: c:=2*c

Exercice 7.4   Les commandes suivantes affectent la valeur $1$ à b : vrai ou faux et pourquoi ?

1. $\square\;$ a:=1:; b=a
2. $\boxtimes\;$ a:=1:; b:=a
3. $\boxtimes\;$ a:=1:; b:='a'
4. $\square\;$ a:=1:; b:="a"
5. $\boxtimes\;$ b:=a/a
6. $\boxtimes\;$ b:=a^0

Exercice 7.5   Les commandes suivantes retournent la valeur exacte 2 : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ 2*a/a
2. $\square\;$ sqrt(4*a^2)/a
3. $\square\;$ simplify(sqrt(4*a^2)/a)
4. $\square\;$ sqrt(4*a^4)/(a*a)
5. $\boxtimes\;$ simplify(sqrt(4*a^4)/(a*a))
6. $\square\;$ expand(sqrt(4*a^4)/(a*a))
7. $\boxtimes\;$ normal(sqrt(4*a^4)/(a*a))
8. $\square\;$ ln(a^2)/ln(a)
9. $\boxtimes\;$ simplify(ln(a^2)/ln(a))
10. $\square\;$ texpand(ln(a^2)/ln(a))
11. $\boxtimes\;$ normal(texpand(ln(a^2)/ln(a)))
12. $\boxtimes\;$ -ln(exp(-2))
13. $\square\;$ 1/exp(-ln(2))
14. $\boxtimes\;$ exp2pow(1/exp(-ln(2)))

Exercice 7.6   Les commandes suivantes définissent la fonction $f$ qui à $x$ associe $x^2$ : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ f(x):=x^2
2. $\boxtimes\;$ f(a):=a^2
3. $\square\;$ f := x^2
4. $\square\;$ f(x):=a^2
5. $\boxtimes\;$ f := a->a^2
6. $\square\;$ f(x):=evalf(x^2)
7. $\square\;$ f(x):=simplify(x^3/x)
8. $\square\;$ f(x):=simplify(x*x*a/a)
9. $\boxtimes\;$ E:=x^2:;f:=unapply(E,x)
10. $\boxtimes\;$ f:=unapply(simplify(x^3/x),x)

Exercice 7.7   Les commandes suivantes définissent la fonction f qui au couple $(x,y)$ associe le produit $xy$ : vrai ou faux et pourquoi ?

1. $\square\;$ f:=x*y
2. $\square\;$ f:=x->x*y
3. $\boxtimes\;$ f:=(a,b)->a*b
4. $\boxtimes\;$ f(x,y):=x*y
5. $\square\;$ f(x,y):=xy
6. $\boxtimes\;$ f:=((x,y)->x)*((x,y)->y)
7. $\square\;$ f:=(x->x)*(y->y)
8. $\boxtimes\;$ f:=unapply(x*y,x,y)
9. $\boxtimes\;$ E:=x*y:;f:=unapply(E,x,y)

Exercice 7.8   Les commandes suivantes définissent la fonction f1 qui à $x$ associe $2*x$ : vrai ou faux et pourquoi ?

1. $\square\;$ f(x):=x^2:; f1(x):=diff(f(x))
2. $\square\;$ f1:=diff(x^2)
3. $\boxtimes\;$ f1:=unapply(diff(x^2),x)
4. $\boxtimes\;$ f(x):=x^2:; f1:=function_diff(f)
5. $\square\;$ f(x):=x^2:; f1:=diff(f)
6. $\square\;$ f(x):=x^2:; f1:=diff(f(x))
7. $\boxtimes\;$ f(x):=x^2:; f1:=unapply(diff(f(x),x),x)
8. $\square\;$ f(x):=x^2:; f1:=x->diff(f(x))

Exercice 7.9   Les commandes suivantes affectent à $A$ l'expression $2*x*y$ : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ A:=diff(x^2*y)
2. $\square\;$ A:=x->diff(x^2*y)
3. $\boxtimes\;$ A:=diff(x^2*y,x)
4. $\square\;$ A:=diff(x^2*y,y)
5. $\square\;$ A:=diff(x*y^2,y)
6. $\boxtimes\;$ A:=normal(diff(x*y^2,y))
7. $\boxtimes\;$ A:=normal(diff(x^2*y^2/2,x,y))
8. $\boxtimes\;$ A:=normal(diff(diff(x^2*y^2/2,x),y))

Exercice 7.10   Les lignes de commande suivantes affichent un losange : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ losange(1,i,pi/3)
2. $\square\;$ losange((1,0),(0,1),pi/3)
3. $\boxtimes\;$ losange(point(1,0),point(0,1),pi/3)
4. $\square\;$ parallelogramme(0,1,1+i)
5. $\boxtimes\;$ parallelogramme(0,1,1/2+i*sqrt(3)/2)
6. $\boxtimes\;$ quadrilatere(0,1,3/2+i*sqrt(3)/2,1/2+i*sqrt(3)/2)
7. $\boxtimes\;$ polygone(0,1,3/2+i*sqrt(3)/2,1/2+i*sqrt(3)/2)
8. $\square\;$ polygonplot(0,1,3/2+i*sqrt(3)/2,1/2+i*sqrt(3)/2)
9. $\square\;$ polygonplot([0,1,3/2,1/2],[0,0,sqrt(3)/2,sqrt(3)/2])
10. $\square\;$ polygone_ouvert(0,1,3/2+i*sqrt(3)/2,1/2+i*sqrt(3)/2)
11. $\boxtimes\;$ polygone_ouvert(0,1,3/2+i*sqrt(3)/2,1/2+i*sqrt(3)/2,0)

Exercice 7.11   Les lignes de commande suivantes affichent le cercle unité : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ cercle(0,1)
2. $\square\;$ arc(-1,1,2*pi)
3. $\boxtimes\;$ arc(-1,1,pi), arc(-1,1,-pi)
4. $\square\;$ plot(sqrt(1-x^2))
5. $\boxtimes\;$ plot(sqrt(1-x^2)), plot(-sqrt(1-x^2))
6. $\boxtimes\;$ plotimplicit(x^2+y^2-1,x,y)
7. $\square\;$ plotparam(cos(t),sin(t))
8. $\boxtimes\;$ plotparam(cos(t)+i*sin(t))
9. $\boxtimes\;$ plotparam(cos(t)+i*sin(t),t)
10. $\boxtimes\;$ plotparam(exp(i*t))
11. $\square\;$ plotparam(cos(t)+i*sin(t),t,0,pi)
12. $\boxtimes\;$ plotparam(cos(t)+i*sin(t),t,0,2*pi)
13. $\boxtimes\;$ plotpolar(1,t)
14. $\boxtimes\;$ plotpolar(1,t,-pi,pi)
15. $\boxtimes\;$ plotpolar(1,t,0,2*pi)

Exercice 7.12   Les commandes suivantes retournent la liste $[1,2,3,4,5]$ : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ [1,2,3,4,5]
2. $\square\;$ op([1,2,3,4,5])
3. $\boxtimes\;$ nop(1,2,3,4,5)
4. $\square\;$ seq(i,i=1..5)
5. $\square\;$ seq(j=1..5)
6. $\square\;$ seq(j,j=1..5)
7. $\square\;$ seq(j,j,1..5)
8. $\boxtimes\;$ seq(j,j,1,5)
9. $\boxtimes\;$ seq(j,j,1,5,1)
10. $\boxtimes\;$ [seq(j,j=1..5)]
11. $\boxtimes\;$ nop(seq(j,j=1..5))
12. $\square\;$ [k$k=1..5]
13. $\boxtimes\;$ [k$(k=1..5)]
14. $\square\;$ [k+1$(k=0..4)]
15. $\boxtimes\;$ [(k+1)$(k=0..4)]
16. $\boxtimes\;$ cumSum([1$5])
17. $\square\;$ sort(5,2,3,1,4)
18. $\boxtimes\;$ sort([5,2,3,1,4])
19. $\square\;$ makelist(k,1,5)
20. $\boxtimes\;$ makelist(x->x,1,5)

Exercice 7.13   Les commandes suivantes retournent la liste $[1.0,0.5,0.25,0.125,0.0625]$ : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ 0.5^[0,1,2,3,4]
2. $\square\;$ 2^(-[0,1,2,3,4])
3. $\boxtimes\;$ 2.0^(-[0,1,2,3,4])
4. $\boxtimes\;$ 2^-evalf([0,1,2,3,4])
5. $\boxtimes\;$ evalf(2^(-[0,1,2,3,4]))
6. $\square\;$ seq(2^(-n),n=0..4)
7. $\boxtimes\;$ evalf([seq(2^(-n),n=0..4)])
8. $\square\;$ 1/evalf(2^n$(n=0..4))
9. $\square\;$ evalf(2^n$(n=0..4))^(-1)
10. $\boxtimes\;$ [evalf(2^n$(n=0..4))]^(-1)
11. $\boxtimes\;$ evalf(nop(2^n$(n=0..4))^(-1))
12. $\boxtimes\;$ a:=[]:; (a:=append(a,0.5^k))$(k=0..4):; a
13. $\square\;$ makelist(k->2^(-k),0,4)
14. $\boxtimes\;$ f:=x->2.0^(-x):; makelist(f,0,4)

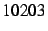
Exercice 7.14   Soit l la liste $[1,0,2,0,3]$. Les lignes de commande suivantes retournent l'entier $10203$ : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ l*10^[4,3,2,1,0]
2. $\square\;$ l*10^[0,1,2,3,4]
3. $\boxtimes\;$ revlist(l)*10^[0,1,2,3,4]
4. $\boxtimes\;$ l*seq(10^n,n,4,0,-1)
5. $\boxtimes\;$ expr(char(sum(l,48)))
6. $\boxtimes\;$ l*nop(seq(10^n,n=(4..0)))
7. $\boxtimes\;$ l*10^nop(j$(j=4..0))
8. $\square\;$ l*10^(j$(j=4..0))
9. $\square\;$ l*10^(j$(j=4..0))
10. $\boxtimes\;$ l*nop(10^j)$(j=4..0))

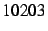
Exercice 7.15   Soit n l'entier $10203$. Les lignes de commande suivantes retournent la liste d'entiers $[1,0,2,0,3]$ : vrai ou faux et pourquoi ?

1. $\square\;$ (floor(n/10^k)-floor(n/10^(k+1))*10)$(k=4..0)
2. $\boxtimes\;$ [(floor(n/10^k)-floor(n/10^(k+1))*10)$(k=4..0)]
3. $\square\;$ seq(iquo(n,10^k)-10*iquo(n,10^(k+1)),k=4..0)
4. $\boxtimes\;$ nop(seq(iquo(n,10^k)-10*iquo(n,10^(k+1)),k=4..0))
5. $\boxtimes\;$ revlist(convert(n,base,10))
6. $\boxtimes\;$ sum(asc(string(n)),-48)
7. $\square\;$ string(n)
8. $\square\;$ mid(string(n),k,1)$(k=0..4)
9. $\square\;$ [mid(string(n),k,1)$(k=0..4)]
10. $\boxtimes\;$ [expr(mid(string(n),k,1))$(k=0..4)]

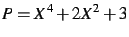
Exercice 7.16   Le polynôme $P=X^4+2X^2+3$ a été affecté par la commande P:=X^4+2*X^2+3. Les lignes de commande suivantes affichent le polynôme réciproque 3*X^4+2*X^2+1 : vrai ou faux et pourquoi ?

1. $\boxtimes\;$ poly2symb(revlist(symb2poly(P)))
2. $\square\;$ X^4*subst(P,X,1/X)
3. $\boxtimes\;$ normal(X^4*subst(P,X,1/X))
4. $\square\;$ normal(subst(P,X,1/X))
5. $\boxtimes\;$ normal(subst(P/X^4,X,1/X))
6. $\boxtimes\;$ normal(X^degree(P)*subst(P,X,1/X))
7. $\boxtimes\;$ getNum(subst(P,X,1/X))
8. $\square\;$ f:=unapply(P,X):; part(f(1/X),1)
9. $\boxtimes\;$ f:=unapply(P,X):; part(normal(f(1/X)),1)

Section : dxcas
Avant : Style de programmation
Après : Exercices