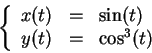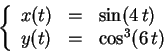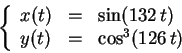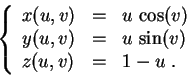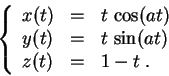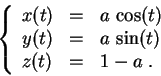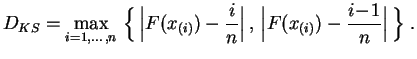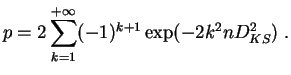Retour : Démarrer en Scilab
Précédent : Calculs sur les lois
Suivant : Index
Il y a souvent plusieurs manières d'obtenir le même résultat en
Scilab. On s'efforcera de choisir les solutions les plus compactes,
c'est-à-dire celles qui utilisent au mieux le langage matriciel.
Exercice 1
Ecrire (sans utiliser de boucle) les vecteurs suivants :
- Nombres de
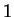 à
à 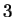 par pas de
par pas de 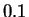 .
.
- Nombres de
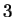 à
à 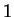 par pas de
par pas de 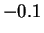 .
.
- Carrés des
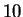 premiers entiers.
premiers entiers.
- Nombres de la forme
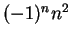 pour
pour
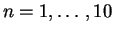 .
.
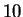 ``0'' suivis de
``0'' suivis de 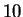 ``
``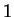 ''.
''.
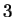 ``0'' suivis de
``0'' suivis de 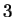 ``
``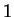 '', suivis de
'', suivis de 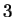 ``
``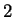 '',...,
suivis de
'',...,
suivis de 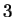 ``
``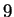 ''.
''.
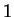 ``
``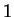 '' suivi de
'' suivi de 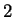 ``
``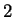 '', suivis de
'', suivis de 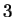 ``
``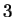 '',...,
suivis de
'',...,
suivis de 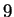 ``
``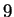 ''.
''.
- ``
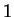 '', suivi de
'', suivi de 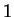 ``0'', suivi de ``2'', suivi de 2 ``0'',...
, suivi de ``
``0'', suivi de ``2'', suivi de 2 ``0'',...
, suivi de ``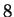 '', suivi de
'', suivi de 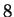 zéros, suivi de ``
zéros, suivi de ``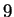 ''.
''.
Exercice 5

- Ecrire la matrice carrée
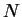 d'ordre
d'ordre 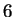 , telle que
, telle que 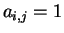 si
si 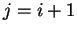 ,
0 sinon.
,
0 sinon.
- Calculer
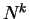 , pour
, pour
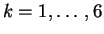 .
.
- Ecrire la matrice
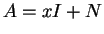 , où
, où 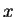 est une variable
de polynôme.
est une variable
de polynôme.
- Calculer
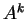 , pour
, pour
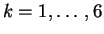 .
.
- Pour
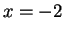 , et
, et 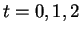 , calculer
, calculer 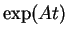 .
.
Exercice 9
Pour chacune des courbes paramétrées suivantes, on choisira un
intervalle de valeurs du paramètre et un pas de discrétisation
assurant une représentation complète et suffisamment lisse.
-
-
-
Exercice 11
Le but de l'exercice est de visualiser un cône de différentes
manières.
- Représenter la surface d'équation
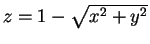 .
.
- Représenter la surface paramétrée définie par :
- Représenter la courbe paramétrée définie par :
(On choisira une valeur de
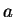 suffisamment grande).
suffisamment grande).
- Représenter la famille de courbes paramétrées définies par :
Exercice 14
Ecrire les fonctions suivantes. Toutes prennent en entrée une fonction
externe
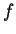
(de
IR dans
IR), et trois valeurs
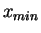
,
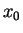
et
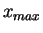
(supposées telles que
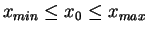
).
derive :
Elle calcule numériquement et représente graphiquement
la dérivée de 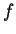 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img117.gif) . Elle retourne la
valeur approchée de
. Elle retourne la
valeur approchée de 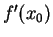 .
.
tangente :
Elle représente la fonction 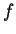 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img117.gif) , elle
superpose sur le même graphique la tangente à
, elle
superpose sur le même graphique la tangente à 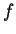 au point
au point 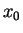 , et
retourne l'équation de cette tangente comme un polynôme du premier
degré.
, et
retourne l'équation de cette tangente comme un polynôme du premier
degré.
araignee :
Elle représente la fonction 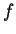 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img117.gif) ,
ainsi que la droite d'équation
,
ainsi que la droite d'équation 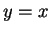 (première bissectrice).
Elle calcule et retourne les
(première bissectrice).
Elle calcule et retourne les 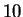 premiers itérés de
premiers itérés de 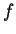 en
en 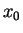 (
(
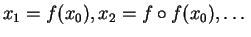 ). Elle représente la suite de
segments, alternativement verticaux et horizontaux, permettant de visualiser
les itérations : segments joignant
). Elle représente la suite de
segments, alternativement verticaux et horizontaux, permettant de visualiser
les itérations : segments joignant 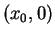 ,
, 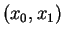 ,
, 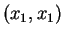 ,
,
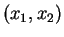 ,
, 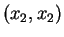 , ...
, ...
newton :
Elle représente la fonction 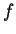 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img117.gif) .
Elle calcule et retourne les dix premiers itérés de la suite définie
à partir de
.
Elle calcule et retourne les dix premiers itérés de la suite définie
à partir de 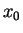 par la méthode de Newton :
par la méthode de Newton :
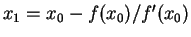 ,
,
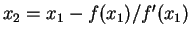 ...Les valeurs de la dérivée sont
approchées. La fonction représente sur le même graphique les
segments permettant de visualiser les iterations : segments joignant
...Les valeurs de la dérivée sont
approchées. La fonction représente sur le même graphique les
segments permettant de visualiser les iterations : segments joignant
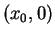 ,
,
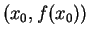 ,
, 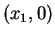 ,
,
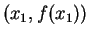 ,
, 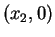 ,
,
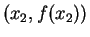 ,...
,...
Exercice 16
Ecrire une fonction
inversion qui simule un échantillon d'une
loi de probabilité continue par la méthode d'inversion. Les
arguments de la fonction sont les deux
entiers donnant la taille de la matrice à engendrer, et la fonction
externe
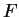
(supposée être une fonction de répartition).
Pour simuler la loi de fonction de répartition
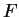
, on appelle un
nombre au hasard
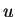
sur
![$ [0,1]$](img7.gif)
et on retourne le réel
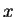
tel que
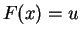
.
- Ecrire la fonction. Pour résoudre l'équation
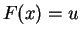 , on pourra
utiliser
, on pourra
utiliser fsolve, ou coder une résolution par dichotomie.
- Tester la fonction en utilisant des fonctions de répartition de
lois usuelles (fonctions
cdf*). Comparer le temps d'exécution
avec celui du générateur grand.
Exercice 17
Ecrire une fonction
kolm_smir pour le test de
Kolmogorov-Smirnov. La fonction prend en entrée un échantillon
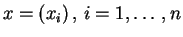
et une fonction externe
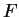
, supposée être une fonction de répartition.
- Elle trie l'échantillon par ordre croissant pour produire la série
des statistiques d'ordre. Elle représente graphiquement les
points d'abscisse
 , et d'ordonnée les
statistiques d'ordre
, et d'ordonnée les
statistiques d'ordre
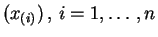 . Elle superpose au
même graphique la représentation de
. Elle superpose au
même graphique la représentation de 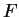 .
.
- Elle calcule (sans utiliser de boucle) la distance de
Kolmogorov-Smirnov entre la distribution
théorique et la distribution observée, par la formule :
Elle retourne la p-valeur du test de Kolmogorov-Smirnov, comme valeur
approchée de la somme :
- Tester la fonction
kolm_smir sur des lois usuelles en utilisant
d'abord le générateur grand, puis la fonction
inversion de l'exercice précédent.
Exercice 18
Ecrire une fonction
fisher_student prenant en entrée deux
echantillons (vecteurs de nombres), et appliquant les tests de Fisher
et Student à ces deux échantillons.
- La fonction calcule les moyennes et variances empiriques des deux
échantillons, ainsi que les statistiques des deux tests.
- Elle retourne la p-valeur des deux tests (bilatéraux).
Exercice 19
Ecrire une fonction
anova prenant en entrée trois
echantillons (vecteurs de nombres), et réalisant une analyse de
variance de ces échantillons.
- La fonction calcule les moyennes et variances empiriques des trois
échantillons, la variance expliquée et la variance résiduelle.
- Elle retourne la p-valeur du test d'analyse de variance pour
l'ensemble des trois échantillons, ainsi que pour chacun des trois
couples d'échantillons.
Retour : Démarrer en Scilab
Précédent : Calculs sur les lois
Suivant : Index
© B. Ycart (2001)
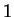 à
à 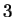 par pas de
par pas de 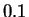 .
.
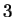 à
à 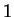 par pas de
par pas de 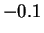 .
.
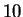 premiers entiers.
premiers entiers.
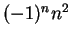 pour
pour
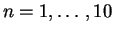 .
.
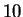 ``0'' suivis de
``0'' suivis de 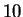 ``
``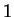 ''.
''.
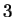 ``0'' suivis de
``0'' suivis de 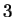 ``
``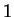 '', suivis de
'', suivis de 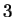 ``
``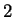 '',...,
suivis de
'',...,
suivis de 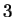 ``
``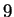 ''.
''.
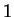 ``
``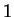 '' suivi de
'' suivi de 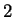 ``
``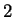 '', suivis de
'', suivis de 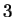 ``
``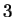 '',...,
suivis de
'',...,
suivis de 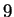 ``
``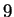 ''.
''.
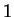 '', suivi de
'', suivi de 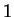 ``0'', suivi de ``2'', suivi de 2 ``0'',...
, suivi de ``
``0'', suivi de ``2'', suivi de 2 ``0'',...
, suivi de ``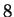 '', suivi de
'', suivi de 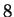 zéros, suivi de ``
zéros, suivi de ``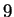 ''.
''.