Section : Statistiques en Scilab
Précédent : Analyse de données
Suivant : Exercices
Scilab propose des fonctions cdf*, à partir desquelles
on retrouve la fonction de répartition, la densité et la fonction quantile
des lois les plus courantes. Ces fonctions sont les suivantes.
| Lois usuelles |
cdfbet |
lois béta |
cdfbin |
lois binomiales |
cdfchi |
lois du chi-deux |
cdfchn |
lois du chi-deux décentrées |
cdff |
lois de Fisher |
cdffnc |
lois de Fisher décentrées |
cdfgam |
lois gamma |
cdfnbn |
lois binomiales négatives |
cdfnor |
lois normales unidimensionnelles |
cdfpoi |
lois de Poisson |
cdft |
lois de Student |
Les familles de lois de
probabilité classiques dépendent de un, deux voire trois paramètres.
Pour chaque valeur du ou des paramètres, la fonction de répartition de
la loi correspondante est déterminée de façon unique.
C'est une fonction qui à une valeur réelle 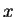 associe une probabilité
associe une probabilité
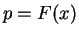 . L'inverse de la fonction de répartition est la
fonction quantile, qui à une probabilité
. L'inverse de la fonction de répartition est la
fonction quantile, qui à une probabilité 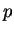 associe le
associe le 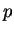 -quantile
-quantile 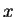 .
Entrent donc en jeu :
.
Entrent donc en jeu :
- les valeurs des paramètres,
- la valeur du quantile
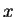
- la valeur de la probabilité
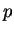 .
.
Toutes les fonctions cdf* sont structurées de façon analogue.
Si on leur donne en entrée toutes les quantités sauf une, ainsi que
l'option appropriée, la fonction retournera la quantité
manquante. Les variables d'entrée étant des vecteurs, on
peut effectuer plusieurs calculs simultanés sur la même loi ou
sur des lois différentes.
Prenons d'abord l'exemple de la loi binomiale (fonction
cdfbin). L'option "PQ" permet de
calculer des valeurs de fonctions de répartition ou de leurs
compléments à 1. A partir de ces valeurs, il est facile par
différences de retrouver les valeurs des probabilités.
Les deux exemples qui suivent concernent la loi binomiale de paramètres
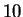 et
et 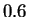 .
.
help cdfbin
[P,Q]=cdfbin("PQ",5,10,0.6,0.4)
c=ones(1,11);
repart=cdfbin("PQ",0:10,10*c,0.6*c,0.4*c)
xbasc()
plot2d2("gnn",[0:10]',repart',5,"111","Repartition",[0,0,11,1])
repart=[0,repart];
probas=repart(2:12)-repart(1:11)
xbasc()
plot2d3("gnn",[0:10]',probas',5,"111","Probabilites",[0,0,10,0.3])
esperance=sum(probas.*[0:10])
L'option "S" permet de calculer les valeurs de la
fonction quantile (interpolée).
cdfbin("S",10,0.2,0.8,0.6,0.4)
p=[0.1:0.1:1];
c=ones(p);
cdfbin("S",10*c,p,1-p,0.6*c,0.4*c)
Les autres options "Xn" et "PrOmpr"
permettent de retouver un paramètre de la loi
connaissant l'autre paramètre et une valeur
de la fonction de répartition.
Voici maintenant l'exemple de la loi normale (fonction
cdfnor). Là encore l'option "PQ"
permet de calculer la fonction de répartition. Sa différentielle
discrète est une approximation de la densité.
help cdfnor
[P,Q] = cdfnor("PQ",1.96,0,1)
x=linspace(-3,3,100);
repart=cdfnor("PQ",x,zeros(x),ones(x));
plot(x,repart)
dens=(repart(2:100)-repart(1:99))*100/6;
x(1)=[];
plot(x,dens)
Pour la fonction quantile, il faut utiliser l'option
"X".
cdfnor("X",0,1,0.975,0.025)
p=[0.01:0.01:0.99];
quant=cdfnor("X",zeros(p),ones(p),p,1-p);
plot(p,quant)
Les options "Mean" et "Std" permettent
de calculer la moyenne ou la variance d'une loi
normale dont on connaît l'autre paramètre et une valeur
de la fonction de répartition.
Les fonctions cdf* suffisent pour toutes les applications de statistique
inférentielle classique : elles permettent de calculer les bornes
des intervalles de confiance, les régions de rejet et les p-valeurs de tous
les tests usuels. Voici par exemple le calcul de l'intervalle de confiance
de niveau 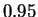 pour l'espérance d'une loi normale,
basé sur la loi de Student.
pour l'espérance d'une loi normale,
basé sur la loi de Student.
n = 30
echant = grand(1,n,"nor",2,3);
moy = mean(echant)
v = mean(echant.*echant)-moy*moy
quantile = cdft("T",n-1,0.975,0.025)
amplitude = quantile*sqrt(v/(n-1))
intervalle = moy+[-1,1]*amplitude
Voici maintenant l'exemple du test du chi-deux. La fonction chideux
ci-dessous prend en entrée une distribution empirique, une distribution
théorique et une taille d'échantillon. Elle calcule la distance du
chi-deux, et retourne la p-valeur du test du chi-deux, pour le cas le plus
simple où aucun paramètre n'a été estimé.
function pv = chideux(de,dt,n)
// retourne la p-valeur du test du chi-deux pour la
// la distribution empirique "de" et la distribution
// theorique "dt", et une taille d'echantillon "n".
c = size(de,"*"); // nombre de classes
d = sum(((de-dt).^2)./dt); // distance du chi-deux
s = n*d; // statistique de test
[p,pv] = cdfchi("PQ",s,c-1); // calcul de la p-valeur
Pour tester cette fonction (placée dans le fichier chideux.sci),
nous utilisons à nouveau les fonctions
ech_dist et freq_emp du fichier lois_discretes.sci.
getf("lois_discretes.sci");
getf("chideux.sci");
n=100; dt = [0.5,0.3,0.2]
ech = ech_dist(1,n,[1,2,3],dt);
de = freq_emp(ech)
pv = chideux(de,dt,n)
Section : Statistiques en Scilab
Précédent : Analyse de données
Suivant : Exercices
© B. Ycart (2001)