Section : demarre_mupad
Précédent : Programmation
Suivant : Domaines

Probabilités et Statistiques

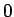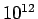MuPAD n'est pas encore aussi bien structuré que Mathematica ou Maple pour ce qui est des probabilités et des statistiques. Le générateur pseudo-aléatoire de base, random, retourne des entiers entre $0$ et $10^{12}$. Sous la forme random(n), il retourne des entiers entre 0 et $\mbox{\tt n}-1$.

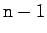alea:= random/1e12;
suite:=alea() $ i=1..100;
moyennes:=_plus(suite[i] $ i=1..n)/n $ n=1..100;
moygraph:=point(n,moyennes[n]) $ n=1..100;
plot2d([Mode=List,[moygraph]]);
plot2d([Mode=List,[point(alea(),alea())$i=1..100]]);

piece:=2*random(2)-1:
pileface:=piece() $ i=1..100;
gains:=_plus(pileface[i] $ i=1..n) $ n=1..100;
gainsgraph:=point(n,gains[n]) $ n=1..100;
plot2d([Mode=List,[polygon(gainsgraph)]]);
moyennes:=gains[n]/n $ n=1..100;
moygraph:=point(n,moyennes[n]) $ n=1..100;
plot2d([Mode=List,[moygraph]]);

Pour les statistiques, quelques fonctions de base sont fournies dans le module stats. On y trouve le calcul de la moyenne, médiane, variance et écart-type, ainsi que les fonctions de répartition de la loi normale, loi du Chi-Deux et loi de Student. On en déduit les densités correspondantes en dérivant par diff, les quantiles en inversant numériquement la fonction de répartition. Il faut noter que la commande export ne fonctionne pas pour ce module, à cause d'une collision malheureuse entre la fonction stats::normal (fonction de répartition de la loi normale) et la fonction du noyau normal (forme normale d'une expression).

?stats::*
?stats::normal
stats::normal(1.96);
stats::normal(-2.3263);
diff(stats::normal(x),x);
plotfunc(stats::Tdist(x,5),
     stats::Tdist(x,10),
     stats::normal(x),x=[-3,3]);

export(numeric):
newton(stats::normal(x)=0.975,x);
newton(stats::Tdist(x,5)=0.975,x);
newton(ChiSquare(x,5)=0.975,x);
newton(ChiSquare(x,5)=0.975,x=3..10);

Il est utile de disposer d'un certain nombre de fonctions de base, pour la génération d'échantillons aléatoires, et la représentation graphique. Les exemples suivants utilisent les fonctions données dans la section précédente. On les suppose rassemblées dans le fichier probastat.mu.

read("probastat.mu"):
pf:=ech_ber(1000,0.3):
frequences(pf);
d:=[random(6)()+1 $ i=1..1000]:
freq:=frequences(d);
plotlib::dataplot(Column,[[freq[i][2]$i=1..6]]);

bin:= _plus(ech_ber(4,0.5)) $ i=1..1000:
freq:=frequences(bin);
plotlib::dataplot(Column,[[freq[i][2]$i=1..6]]);

x:=ech_uni(1000):
frequence_classe(x,0.3,0.7);
histogramme(x,[0,0.1,0.3,0.6,1]);
histo_reg(x,0,1,10);

x:=ech_uni(1000):
expo:=map(x,-ln);
histogramme(expo,[0,0.2,0.6,1.5,3,5]);
histo_reg(expo,0,5,20);

x:=ech_uni(1000):
y:=ech_uni(1000):
tri1:=[min(x[i],y[i]) $ i=1..1000];
histo_reg(tri1,0,1,10);
tri2:=[x[i]-y[i] $ i=1..1000];
histo_reg(tri2,-1,1,10];

x:=ech_nor(1000):
frequence_classe(x,0.2,1.5);
stats::normal(1.5)-stats::normal(0.2);
histo_reg(x,-3,3,20);

x:=ech_uni(1000):
y:=ech_uni(1000):
nuage(x,y);

x:=ech_uni(1000):
y:=ech_uni(1000):
tri1:=[min(x[i],y[i]) $ i=1..1000];
x:=ech_uni(1000):
y:=ech_uni(1000):
tri2:=[max(x[i],y[i]) $ i=1..1000];
nuage(tri1,tri2);

x:=ech_nor(1000):
y:=ech_nor(1000):
nuage(x,y);
r:=0.8;
z:=sqrt(1-r^2)*x + r*y:
nuage(x,z);
r:=-0.8;
z:=sqrt(1-r^2)*2*x + r*y:
nuage(x,z);