Dans cette section, nous étudions le cas des fonctions monotones et
des fonctions continues.
Soit  une fonction bornée de
une fonction bornée de ![$ [a,b]$](img4.gif) dans
dans
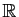 . L'idée est de
considérer des encadrements de
. L'idée est de
considérer des encadrements de  par des fonctions en escalier
par des fonctions en escalier
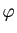 et
et 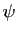 , comme sur la
figure 6.
, comme sur la
figure 6.
Figure 6:
Encadrement d'une fonction  par des fonctions en escalier.
par des fonctions en escalier.
|
|
On peut supposer que les fonctions en escalier 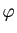 et
et 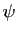 sont exprimées au moyen de la même subdivision
sont exprimées au moyen de la même subdivision
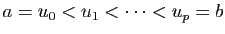 :
sinon il est toujours possible de redécouper
les subdivisions qui les définissent, pour arriver à une
subdivision commune (comme les valeurs
:
sinon il est toujours possible de redécouper
les subdivisions qui les définissent, pour arriver à une
subdivision commune (comme les valeurs
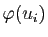 ,
, 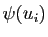 ne
jouent pas de rôle dans les intégrales, on choisira par exemple
ne
jouent pas de rôle dans les intégrales, on choisira par exemple
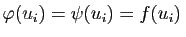 ). On aura donc :
). On aura donc :
Dans cette situation, l'erreur due
à l'encadrement de l'aire est précisément :
C'est l'aire des rectangles grisés sur la figure 6.
Nous commençons par un critère d'intégrabilité, qui sera ensuite
appliqué aux fonctions monotones, puis aux fonctions
continues.
Lemme 1
Toute fonction intégrable sur ![$ [a,b]$](img4.gif) est bornée.
est bornée.
Démonstration : Soit  une fonction intégrable sur
une fonction intégrable sur ![$ [a,b]$](img4.gif) .
Il existe des réels
.
Il existe des réels 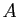 et
et 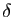 tels que
tels que
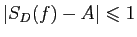 pour toute subdivision
pour toute subdivision 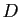
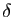 -fine. En
remplaçant éventuellement
-fine. En
remplaçant éventuellement 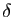 par une valeur plus petite,
on peut supposer que
par une valeur plus petite,
on peut supposer que
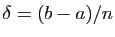 pour
pour
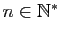 .
.
Soit
![$ D=\{([a_{i-1},a_i],x_i)\}_{1\leqslant i\leqslant n}$](img93.gif) la subdivision pointée définie par
la subdivision pointée définie par
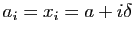 .
Donc
.
Donc 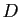 est
est 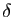 -fine (et régulière).
-fine (et régulière).
Soit 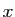 un point quelconque de
un point quelconque de ![$ [a,b]$](img4.gif) .
Il existe un indice
.
Il existe un indice 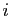 tel que
tel que
![$ x\in [a_{i-1},a_i]$](img250.gif) .
Soit
.
Soit 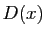 la subdivision pointée obtenue à
partir de
la subdivision pointée obtenue à
partir de 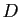 en remplaçant
en remplaçant 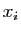 par
par 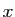 et en ne changeant rien d'autre. Comme
et en ne changeant rien d'autre. Comme 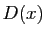 et
et
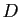 sont toutes deux
sont toutes deux 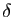 -fines,
-fines,
Or,
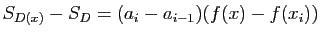 . On en déduit :
. On en déduit :
Finalement, on obtient la borne uniforme suivante : pour tout 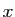 dans
dans ![$ [a,b]$](img4.gif) ,
,

Définition 6
Soit
![$ f:[a,b]\to\mathbb{R}$](img226.gif) une
fonction. On note
une
fonction. On note
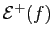 l'ensemble des
fonctions en escalier
l'ensemble des
fonctions en escalier 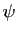 telles que
telles que
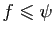 , et
, et
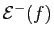 l'ensemble des
fonctions en escalier
l'ensemble des
fonctions en escalier 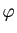 telles que
telles que
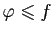 .
.
Proposition 7
Soit
![$ f:[a,b]\to\mathbb{R}$](img226.gif) une
fonction. La fonction
une
fonction. La fonction  est intégrable sur
est intégrable sur ![$ [a,b]$](img4.gif) si et seulement si
pour tout
si et seulement si
pour tout
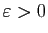 , il existe deux
fonctions
, il existe deux
fonctions
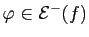 et
et
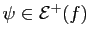 telles que :
telles que :
Dans ce cas,
on a :
Démonstration : Notons 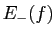 (respectivement :
(respectivement : 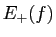 )
l'ensemble des intégrales des fonctions
)
l'ensemble des intégrales des fonctions
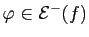 (respectivement :
(respectivement :
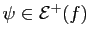 ).
Si
).
Si
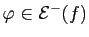 et
et
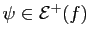 ,
alors
,
alors
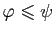 , donc :
, donc :
Par conséquent, tout élément 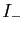 de
de 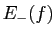 et tout élément
et tout élément 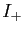 de
de
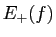 sont tels que
sont tels que
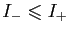 .
.
La condition de la proposition
assure que 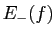 et
et 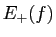 ne sont pas vides et que,
pour tout
ne sont pas vides et que,
pour tout
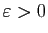 , il existe un élément de
, il existe un élément de
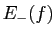 et un élément de
et un élément de 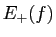 dont la différence est au plus
dont la différence est au plus
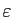 . Ceci entraîne que la borne supérieure de
. Ceci entraîne que la borne supérieure de 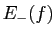 et la
borne inférieure de
et la
borne inférieure de 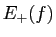 sont égales : notons
sont égales : notons 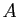 leur valeur
commune.
Fixons
leur valeur
commune.
Fixons
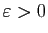 , et choisissons deux fonctions en escalier
, et choisissons deux fonctions en escalier
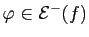 et
et
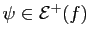 telles que :
telles que :
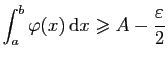
et
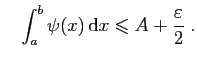
Toutes les fonctions en escalier sont intégrables donc il existe des
réels 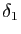 et
et 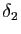 qui sont
qui sont
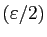 -adaptés pour
-adaptés pour
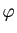 et
et 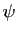 respectivement. Posons
respectivement. Posons
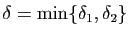 . Soit
. Soit 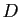 une subdivision
une subdivision
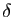 -fine de
-fine de ![$ [a,b]$](img4.gif) . Comme
. Comme 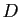 est à la fois
est à la fois 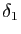 -fine et
-fine et
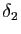 -fine,
-fine,
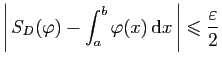
et
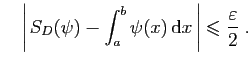
Nous allons vérifier que :
Écrivons :
Dans l'autre sens :
On a montré que  est intégrable et que son intégrale vaut
est intégrable et que son intégrale vaut 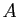 .
.
Dans l'autre sens, supposons que  est intégrable.
Notons
est intégrable.
Notons 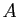 son intégrale. Fixons deux réels
son intégrale. Fixons deux réels
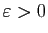 et
et 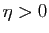 . Il existe un réel
. Il existe un réel 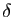 tel que toute subdivision pointée
tel que toute subdivision pointée
![$ D=\{([a_{i-1},a_i],x_i)\}_{1\leqslant i\leqslant n}$](img93.gif)
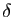 -fine vérifie :
-fine vérifie :
Pour chaque
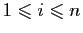 , notons :
, notons :
Il existe
![$ x^+_i\in[a_{i-1},a_i]$](img283.gif) et
et
![$ x^-_i\in[a_{i-1},a_i]$](img284.gif) tels que :
tels que :
Notons
![$ D^+=\{([a_{i-1},a_i],x^+_i)\}_{1\leqslant i\leqslant n}$](img286.gif) et
et
![$ D^-=\{([a_{i-1},a_i],x^-_i)\}_{1\leqslant i\leqslant n}$](img287.gif) .
Les subdivisions pointées
.
Les subdivisions pointées 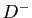 et
et 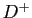 sont
sont 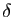 -fines donc
-fines donc
En particulier,
Notons 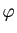 une fonction en escalier telle que
une fonction en escalier telle que
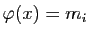 sur chaque intervalle
sur chaque intervalle
![$ ]a_{i-1},a_i[$](img293.gif) et
et
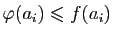 , et
, et 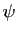 une fonction en escalier telle que
une fonction en escalier telle que
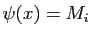 sur chaque intervalle
sur chaque intervalle
![$ ]a_{i-1},a_i[$](img293.gif) et
et
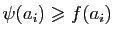 .
.
Par construction,
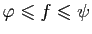 donc
donc
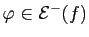 et
et
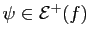 . De plus,
. De plus,
et
En reportant dans ces inégalités notre estimation de l'écart
entre
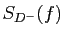 et
et
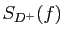 , on voit que :
, on voit que :
Si on choisit
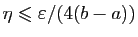 ,
on obtient la condition de l'énoncé.
,
on obtient la condition de l'énoncé.
Théorème 7
Toute fonction monotone de ![$ [a,b]$](img4.gif) dans
dans
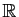 est
intégrable sur
est
intégrable sur ![$ [a,b]$](img4.gif) .
.
Démonstration : Soit  une fonction monotone de
une fonction monotone de ![$ [a,b]$](img4.gif) dans
dans
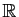 .
Quitte à remplacer
.
Quitte à remplacer  par
par 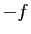 , nous pouvons supposer que
, nous pouvons supposer que  est
croissante. Si
est
croissante. Si  est constante, le résultat est déjà
démontré. Sinon,
est constante, le résultat est déjà
démontré. Sinon,
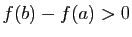 .
Fixons
.
Fixons
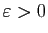 et posons
et posons
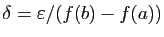 . Soit
. Soit
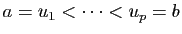 une subdivision
une subdivision 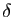 -fine de
-fine de ![$ [a,b]$](img4.gif) .
Définissons les fonctions en escalier
.
Définissons les fonctions en escalier 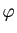 et
et 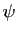 , pour tout
, pour tout
 et pour tout
et pour tout
![$ x\in]u_{i-1},u_{i}[$](img308.gif) par :
par :
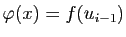
et
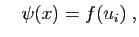
et
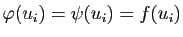 comme déjà convenu. Cela donne :
comme déjà convenu. Cela donne :
L'hypothèse de la proposition 7
est donc vérifiée.
Théorème 8
Toute fonction continue de ![$ [a,b]$](img4.gif) dans
dans
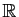 est
intégrable sur
est
intégrable sur ![$ [a,b]$](img4.gif) .
.
Démonstration : Nous admettrons que toute fonction continue sur ![$ [a,b]$](img4.gif) est en fait
uniformément continue. Ce résultat est démontré dans les
compléments du
chapitre Limites et continuité. (Le lecteur intéressé
pourra tout d'abord essayer de se convaincre de la différence
entre la définition de la continuité, suposée connue, et celle
de l'uniforme continuité, rappelée ci-dessous.)
est en fait
uniformément continue. Ce résultat est démontré dans les
compléments du
chapitre Limites et continuité. (Le lecteur intéressé
pourra tout d'abord essayer de se convaincre de la différence
entre la définition de la continuité, suposée connue, et celle
de l'uniforme continuité, rappelée ci-dessous.)
Fixons
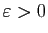 . L'uniforme continuité de
. L'uniforme continuité de  signifie qu'il existe
un réel
signifie qu'il existe
un réel 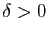 tel
que pour tous
tel
que pour tous 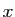 et
et 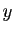 dans l'intervalle
dans l'intervalle ![$ [a,b]$](img4.gif) :
:
Choisissons une subdivision pointée
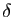 -fine
-fine
![$ D=\{([a_{i-1},a_i],x_i)\}_{1\leqslant i\leqslant n}$](img93.gif) .
Pour tous
.
Pour tous 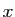 et
et 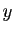 dans l'intervalle
dans l'intervalle
![$ [a_{i-1},a_i]$](img35.gif) ,
,
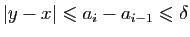 , donc :
, donc :
Comme  est continue sur
est continue sur
![$ [a_{i-1},a_i]$](img35.gif) , elle y atteint sa borne
supérieure et sa borne inférieure. Notons :
, elle y atteint sa borne
supérieure et sa borne inférieure. Notons :
![$\displaystyle m_i = \inf\{ f(x) , x\in [a_{i-1},a_i] \}$](img321.gif)
et
![$\displaystyle \quad
M_i = \sup\{ f(x) , x\in [a_{i-1},a_i] \}\;.
$](img322.gif)
Ce qui précède montre que pour tout
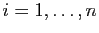 ,
,
Définissons maintenant, pour tout
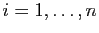 et pour tout
et pour tout
![$ x\in ]a_{i-1},a_i[$](img324.gif) ,
,
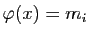
et
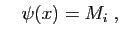
et comme d'habitude
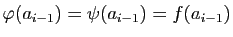 . Les fonctions
. Les fonctions
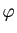 et
et 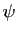 encadrent
encadrent  et :
et :
L'hypothèse de la proposition 7
est donc vérifiée.
Démonstration : Nous savons que l'intégrale définissant 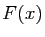 existe pour tout
existe pour tout
![$ x\in[a,b]$](img44.gif) , par le théorème 8.
Nous allons démontrer que la fonction
, par le théorème 8.
Nous allons démontrer que la fonction 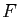 est dérivable sur
est dérivable sur
![$ ]a,b[$](img187.gif) , de dérivée
, de dérivée  . Ceci entraîne le résultat, par
le théorème 4 et la proposition
6.
. Ceci entraîne le résultat, par
le théorème 4 et la proposition
6.
Soient 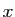 un point de
un point de ![$ ]a,b[$](img187.gif) et
et 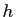 un
réel tel que
un
réel tel que
![$ x+h\in]a,b[$](img335.gif) .
La relation de Chasles donne
.
La relation de Chasles donne
Fixons
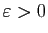 . Puisque
. Puisque  est continue en
est continue en 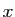 , il existe
, il existe 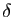 tel que pour
tel que pour
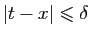 ,
,
Par le théorème 2, pour
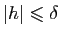 ,
,
En divisant par 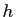 , on obtient :
, on obtient :
D'où le résultat. Nous avons déjà vu que l'intégrale d'une fonction positive ou
nulle est positive ou nulle. Si de plus la fonction est
continue et non identiquement nulle, son intégrale est
strictement positive ; on utilise souvent ce résultat sous la forme
suivante.
Nous avons déjà vu que l'intégrale d'une fonction positive ou
nulle est positive ou nulle. Si de plus la fonction est
continue et non identiquement nulle, son intégrale est
strictement positive ; on utilise souvent ce résultat sous la forme
suivante.
Démonstration : Nous allons démontrer la contraposée : si 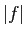 n'est pas
identiquement nulle, alors son intégrale est strictement positive.
Soit
n'est pas
identiquement nulle, alors son intégrale est strictement positive.
Soit 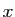 un point de
un point de ![$ [a,b]$](img4.gif) tel que
tel que  . Puisque
. Puisque  est
continue en
est
continue en 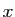 ,
, 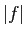 l'est aussi, et il existe
l'est aussi, et il existe 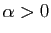 tel que pour tout
tel que pour tout
![$ t\in [x-\alpha,x+\alpha]$](img345.gif) ,
,
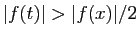 . Donc :
. Donc :
 Toujours en utilisant la monotonie, la valeur de l'intégrale peut être
encadrée à l'aide du minimum et du maximum de
Toujours en utilisant la monotonie, la valeur de l'intégrale peut être
encadrée à l'aide du minimum et du maximum de  sur l'intervalle
sur l'intervalle
![$ [a,b]$](img4.gif) . Notons :
. Notons :
![$\displaystyle m=\inf\{f(x) ,\;x\in[a,b]\}$](img348.gif)
et
![$\displaystyle \quad
M=\sup\{f(x) ,\;x\in[a,b]\}\;.
$](img349.gif)
Alors,
Si on divise ces inégalités par la longueur de l'intervalle, on
obtient :
Il faut comprendre
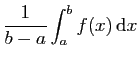 comme la valeur moyenne de la fonction sur l'intervalle.
Le théorème de la moyenne dit que cette valeur moyenne est
atteinte sur l'intervalle.
comme la valeur moyenne de la fonction sur l'intervalle.
Le théorème de la moyenne dit que cette valeur moyenne est
atteinte sur l'intervalle.
Théorème 10
Si  est continue sur
est continue sur ![$ [a,b]$](img4.gif) , il existe
, il existe
![$ c\in [a,b]$](img353.gif) tel que :
tel que :
Géométriquement, 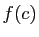 est la hauteur du rectangle au-dessus de
est la hauteur du rectangle au-dessus de
![$ [a,b]$](img4.gif) , dont la surface est égale à l'intégrale de
, dont la surface est égale à l'intégrale de  sur
sur ![$ [a,b]$](img4.gif) (figure 7).
(figure 7).
Figure 7:
Illustration du théorème de la moyenne.
|
|
Démonstration : Soit 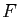 une primitive de
une primitive de  (théorème
9) :
(théorème
9) : 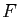 est dérivable et a pour
dérivée
est dérivable et a pour
dérivée  . De plus :
. De plus :
Le théorème des accroissements finis dit que le taux
d'accroissement de 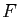 sur
sur ![$ [a,b]$](img4.gif) est égal à la valeur de la
dérivée en un point
est égal à la valeur de la
dérivée en un point 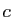 de
de ![$ ]a,b[$](img187.gif) . D'où le résultat.
. D'où le résultat.
Les théorèmes 7 et
8 s'étendent sans difficulté aux cas des
fonctions monotones par morceaux et des fonctions continues par morceaux.
Proposition 9
Toute fonction monotone par morceaux est
intégrable sur ![$ [a,b]$](img4.gif) . Toute fonction
continue par morceaux est
intégrable sur
. Toute fonction
continue par morceaux est
intégrable sur ![$ [a,b]$](img4.gif) .
.
Démonstration : L'hypothèse affirme que sur chaque intervalle
![$ [a_{i-1},a_i]$](img35.gif) , la
fonction considérée diffère d'une fonction monotone
(respectivement : continue) au plus aux extrémités de
l'intervalle.
Elle est donc intégrable sur
, la
fonction considérée diffère d'une fonction monotone
(respectivement : continue) au plus aux extrémités de
l'intervalle.
Elle est donc intégrable sur
![$ [a_{i-1},a_i]$](img35.gif) , d'après le corollaire
1.
D'où le résultat,
par la relation de Chasles.
, d'après le corollaire
1.
D'où le résultat,
par la relation de Chasles. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
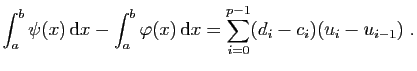
![]() la subdivision pointée définie par
la subdivision pointée définie par
![]() .
Donc
.
Donc ![]() est
est ![]() -fine (et régulière).
-fine (et régulière).
![]() un point quelconque de
un point quelconque de ![]() .
Il existe un indice
.
Il existe un indice ![]() tel que
tel que
![]() .
Soit
.
Soit ![]() la subdivision pointée obtenue à
partir de
la subdivision pointée obtenue à
partir de ![]() en remplaçant
en remplaçant ![]() par
par ![]() et en ne changeant rien d'autre. Comme
et en ne changeant rien d'autre. Comme ![]() et
et
![]() sont toutes deux
sont toutes deux ![]() -fines,
-fines,
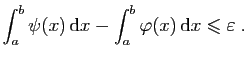
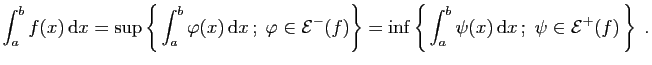
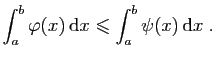
![]() et
et ![]() ne sont pas vides et que,
pour tout
ne sont pas vides et que,
pour tout
![]() , il existe un élément de
, il existe un élément de
![]() et un élément de
et un élément de ![]() dont la différence est au plus
dont la différence est au plus
![]() . Ceci entraîne que la borne supérieure de
. Ceci entraîne que la borne supérieure de ![]() et la
borne inférieure de
et la
borne inférieure de ![]() sont égales : notons
sont égales : notons ![]() leur valeur
commune.
Fixons
leur valeur
commune.
Fixons
![]() , et choisissons deux fonctions en escalier
, et choisissons deux fonctions en escalier
![]() et
et
![]() telles que :
telles que :
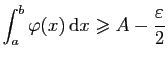 et
et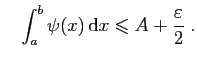
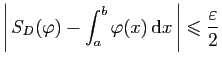 et
et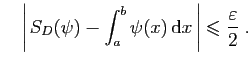
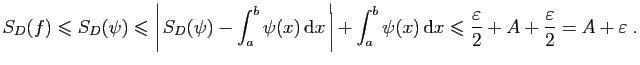
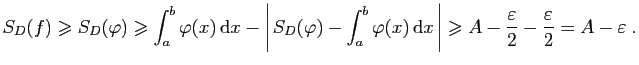
![]() est intégrable.
Notons
est intégrable.
Notons ![]() son intégrale. Fixons deux réels
son intégrale. Fixons deux réels
![]() et
et ![]() . Il existe un réel
. Il existe un réel ![]() tel que toute subdivision pointée
tel que toute subdivision pointée
![]()
![]() -fine vérifie :
-fine vérifie :
![]() donc
donc
![]() et
et
![]() . De plus,
. De plus,
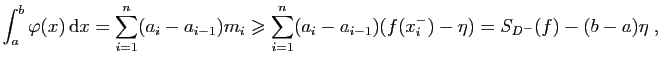
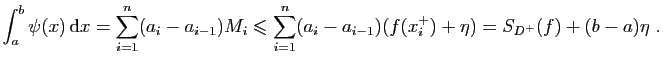
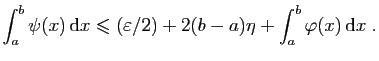
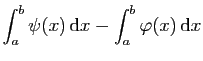
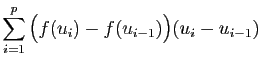
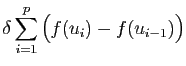
![]() est en fait
uniformément continue. Ce résultat est démontré dans les
compléments du
chapitre Limites et continuité. (Le lecteur intéressé
pourra tout d'abord essayer de se convaincre de la différence
entre la définition de la continuité, suposée connue, et celle
de l'uniforme continuité, rappelée ci-dessous.)
est en fait
uniformément continue. Ce résultat est démontré dans les
compléments du
chapitre Limites et continuité. (Le lecteur intéressé
pourra tout d'abord essayer de se convaincre de la différence
entre la définition de la continuité, suposée connue, et celle
de l'uniforme continuité, rappelée ci-dessous.)
![]() . L'uniforme continuité de
. L'uniforme continuité de ![]() signifie qu'il existe
un réel
signifie qu'il existe
un réel ![]() tel
que pour tous
tel
que pour tous ![]() et
et ![]() dans l'intervalle
dans l'intervalle ![]() :
:
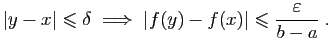
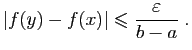
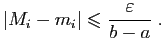
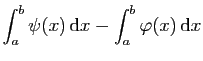
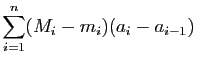
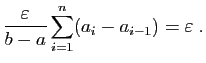
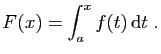
![]() un point de
un point de ![]() et
et ![]() un
réel tel que
un
réel tel que
![]() .
La relation de Chasles donne
.
La relation de Chasles donne
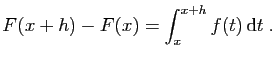
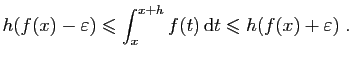
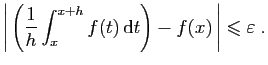
![$\displaystyle \int_a^b \vert f(x)\vert \mathrm{d}x =0\; \Longrightarrow\;
\Big( \forall x\in[a,b] ,\;f(x)=0 \Big)\;.
$](img342.gif)
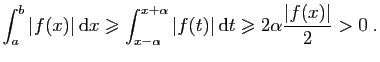
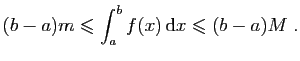
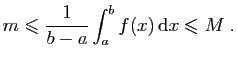
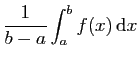 comme la valeur moyenne de la fonction sur l'intervalle.
Le théorème de la moyenne dit que cette valeur moyenne est
atteinte sur l'intervalle.
comme la valeur moyenne de la fonction sur l'intervalle.
Le théorème de la moyenne dit que cette valeur moyenne est
atteinte sur l'intervalle.
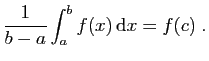
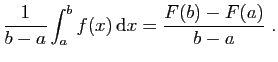
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales