QCM

Donnez-vous une heure pour répondre à ce questionnaire. Les 10 questions sont indépendantes. Pour chaque question 5 affirmations sont proposées, parmi lesquelles 2 sont vraies et 3 sont fausses. Pour chaque question, cochez les 2 affirmations que vous pensez vraies. Chaque question pour laquelle les 2 affirmations vraies sont cochées rapporte 2 points.

Question 1   Soit $f$ l'application de $[0,1]$ dans $[0,1]$ qui à $x$ associe $x^2$. Soit $\gamma\in[0,1]$ un réel. Pour tout $i=0,\ldots,10$, on pose $a_{i}=i/10$. Pour $i=1,\ldots, 10$, on pose $x_i=a_{i-1}+\gamma/10$. On note $D_\gamma$ la subdivision pointée $D_\gamma=\{([a_{i-1},a_i],x_i)\}_{1\leqslant i\leqslant 10}$ et $S_\gamma$ la somme de Riemman associée à $f$ sur $D_\gamma$.

$S_0=\displaystyle{\frac{1}{1000}\sum_{i=0}^{9} i^2}$.

$S_0=\displaystyle{\sum_{i=1}^{10} \frac{1}{i^2}}$.

$S_1=\displaystyle{\frac{1}{10}\sum_{i=0}^{9} \frac{i^2}{100}}$.

$S_{1/2}=\displaystyle{\frac{1}{100}\sum_{i=0}^{9} \frac{(2i+1)^2}{10}}$.

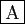
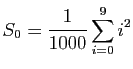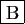
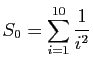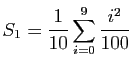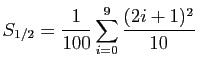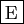
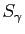$S_\gamma$ est fonction croissante de $\gamma$.

Question 2   Soit $f$ l'application de $[0,1]$ dans $[0,1]$ qui à $x$ associe $x^2$. Soit $n$ un entier. La somme $S_n$ est une somme de Riemann associée à $f$ sur $[-1,1]$.

$S_n=\displaystyle{\frac{1}{2n}\sum_{i=-n}^n \frac{i^2}{n^2}}$.

$S_n=\displaystyle{\frac{1}{n}\sum_{i=0}^n \frac{(2i-1)^2}{n^2}}$.

$S_n=\displaystyle{\frac{1}{n}\sum_{i=-n}^n \frac{i^2}{n^2}}$.

$S_n=\displaystyle{\frac{1}{n}\sum_{i=-n}^{n-1} \frac{i^2}{n^2}}$.

$S_n=\displaystyle{\frac{1}{n}\sum_{i=1}^n \frac{(2i-n)^2}{n^2}}$.

Question 3   Soit $f$ une fonction, définie sur un intervalle $[a,b]$ de $\mathbb{R}$, intégrable sur $[a,b]$. Soit $S$ un ensemble fini de points de $[a,b]$.

Si $f(x)=0$ pour tout $x$ dans $S$, alors $${\int_a^b f(x) \mathrm{d}x=0}$$.

Si $f(x)=1$ pour tout $x$ dans $S$, alors $${\int_a^b f(x) \mathrm{d}x=b-a}$$.

Si $f(x)=x$ pour tout $x$ dans $[a,b]\setminus S$, alors $${\int_a^b f(x) \mathrm{d}x=b-a}$$.

Si $f(x)=0$ pour tout $x$ dans $[a,b]\setminus S$, alors $${\int_a^b f(x) \mathrm{d}x=0}$$.

Si $f(x)=x$ pour tout $x$ dans $[a,b]\setminus S$, alors $${\int_a^b f(x) \mathrm{d} x=(b^2-a^2)/2}$$.

Question 4   La proposition est vraie pour toute fonction $f$ de $[0,1]$ dans $[0,1]$, intégrable sur $[0,1]$.

$${\int_0^1 f^2(x) \mathrm{d}x \leqslant \int_0^1 f(x) \mathrm{d}x}$$.

$${\int_0^1 f^2(x) \mathrm{d}x \leqslant \frac{1}{2}}\;.$$

$${\int_0^1 f^2(x) \mathrm{d}x \leqslant \int_0^1 1-f(x) \mathrm{d}x}$$.

$${\int_0^1 1-f(x) \mathrm{d}x \leqslant \left\vert 1-\int_0^1 f(x) \mathrm{d}x\right\vert}$$.

$${\int_0^1 f^3(x) \mathrm{d}x \leqslant \int_0^1 f^2(x) \mathrm{d}x}$$.

Question 5   La proposition est vraie pour toute fonction $f$ de $[-1,1]$ dans $[-1,1]$, intégrable sur $[-1,0]$ et $[0,1]$.

$${\int_{0}^1 f(x) \mathrm{d}x = \int_{-1}^1 f(x) \mathrm{d}x+\int_0^{-1}f(x) \mathrm{d}x}$$.

$${\int_{0}^1 f(x) \mathrm{d}x = \int_{-1}^1 f(x) \mathrm{d}x+\int_{-1}^{0}f(x) \mathrm{d}x}$$.

$${\int_{0}^1 f(x) \mathrm{d}x \leqslant \int_{-1}^1 f(x)}$$.

$${\int_{-1}^1 (1-f(x)) \mathrm{d}x = 1-\int_{-1}^1 f(x) \mathrm{d}x}$$.

$${-2\leqslant \int_{-1}^1 f(x) \mathrm{d}x \leqslant 2}$$.

Question 6   Soit $f$ une fonction de $[0,1]$ dans $[0,1]$, admettant une primitive. Pour tout $c\in\mathbb{R}$, on note $F_c$ la primitive de $f$ telle que $F(0)=c$.

$\forall x\in [0,1]\;,\quad F_{-1}(x)\leqslant 0$.

$\forall c\in [0,1]\;,\quad F_{c}(x)\leqslant 1$.

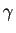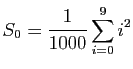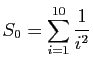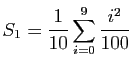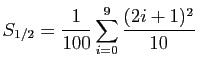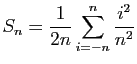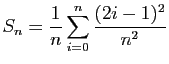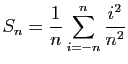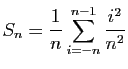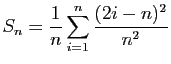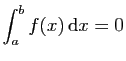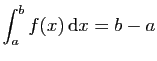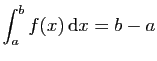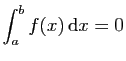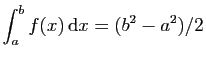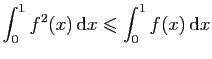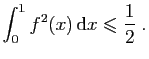
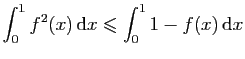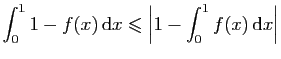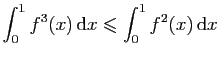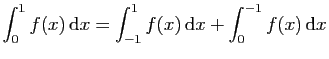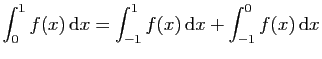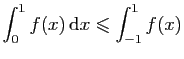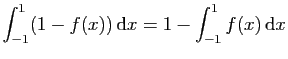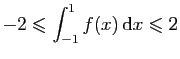$\forall c\in [0,1]\;,\quad \displaystyle{\int_c^1 f(x) \mathrm{d}x = F_c(1)}$.

$\forall c\in [0,1] ,\;\forall x\in [0,1]\;,\quad F_{c}(x)-F_{-c}(x)=2c$.

$\forall c\in [0,1] ,\;\forall x\in [0,1] ,\; \displaystyle{\int_0^c f(x) \mathrm{d}x = F_c(0)}$.

Question 7    

$${\int_0^\pi x\sin(x) \mathrm{d}x = \int_0^\pi\cos(x) \mathrm{d}x}$$.

$${\int_0^{\pi} x\cos(x) \mathrm{d}x = -\int_0^\pi\sin(x) \mathrm{d}x}$$.

$${\int_0^{\pi/2} \cos^2(x) \mathrm{d}x = \int_0^{\pi/2}x\sin(2x) \mathrm{d}x}$$.

$${\int_0^{\pi/2} \sin^2(x) \mathrm{d}x = \frac{\pi}{2}+\int_0^{\pi/2}x\sin(2x) \mathrm{d}x}$$.

$${\int_0^{\pi} x\cos(x) \mathrm{d}x = \int_0^{\pi}x^2\sin(x) \mathrm{d}x}$$.

Question 8   La proposition est vraie pour toute fonction $f$ de $[0,1]$ dans $[0,1]$, intégrable sur $[0,1]$.

$${\int_0^1 f(x) \mathrm{d}x = \int_0^1f(x^2) \mathrm{d}x}$$.

$${\int_0^1 f(x) \mathrm{d}x = \int_0^\pi f(\sin(x))\cos(x) \mathrm{d}x}$$.

$${\int_0^1 f(x) \mathrm{d}x = \int_0^1f(1-x) \mathrm{d}x}$$.

$${\int_0^1 f(x) \mathrm{d}x = \int_0^{\pi/2} f(\cos(x))\sin(x) \mathrm{d}x}$$.

$${\int_0^1 f(x) \mathrm{d}x = \frac{1}{2}\int_0^{1/2} f(2x) \mathrm{d}x}$$.

Question 9   La proposition est vraie pour toute fonction $f$ continue sur $[-1,1]$.

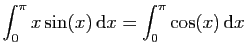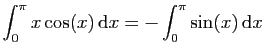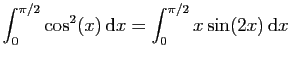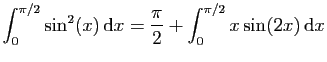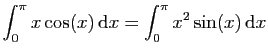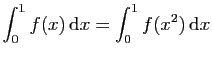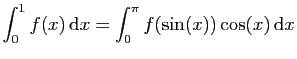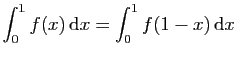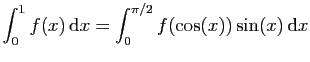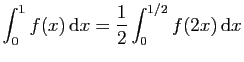$\exists c\in [-1,1]\;,\quad \displaystyle{\int_{-1}^{1} f(x) \mathrm{d}x =2f(c)}$.

$\exists c\in [-1,1]\;,\quad \displaystyle{\int_{0}^{1} f(x) \mathrm{d}x =2f(c)}$.

$\exists c\in [0,1]\;,\quad \displaystyle{\int_{-1}^{1} f(x) \mathrm{d}x =2f(c)}$.

$\inf\{f(x) ,\;x\in[-1,1]\} \leqslant \displaystyle{\int_0^1 f(x) \mathrm{d}x}\leqslant \sup\{f(x) ,\;x\in[-1,1]\}$

$\inf\{f(x) ,\;x\in[-1,1]\} \leqslant \displaystyle{\int_{-1}^1 f(x) \mathrm{d}x}\leqslant \sup\{f(x) ,\;x\in[-1,1]\}$

Question 10   Soit $f$ une fonction de $[0,1]$ dans $\mathbb{R}$.

Si $f$ n'est pas continue sur $[0,1]$, alors $f$ n'est pas intégrable sur $[0,1]$.

Si $f$ est décroissante sur $[0,1]$, alors $f$ est intégrable sur $[0,1]$.

Si $f$ n'est pas intégrable sur $[0,1]$, alors $f$ n'est monotone sur aucun intervalle inclus dans $[0,1]$.

Si $f$ est continue sur $[0,1]$, sauf en un nombre fini de points, alors $f$ est intégrable sur $[0,1]$.

Si $f$ diffère d'une fonction croissante sur $[0,1]$ en un nombre dénombrable de points, alors $f$ est intégrable sur $[0,1]$.