Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit 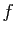 une fonction définie sur un intervalle
une fonction définie sur un intervalle ![$ [a,b]$](img4.gif) de
de
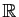 et
intégrable sur
et
intégrable sur ![$ [a,b]$](img4.gif) . Soit
. Soit
![$ D=\{([a_{i-1},a_i],x_i)\}_{1\leqslant i\leqslant n}$](img93.gif) une subdivision pointée
de
une subdivision pointée
de ![$ [a,b]$](img4.gif) .
.
- Qu'appelle-t-on pas de la subdivision
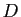 ?
?
- Qu'appelle-t-on somme de Riemann associée à
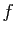 sur
sur 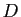 ?
?
- Si
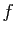 est constante sur
est constante sur ![$ [a,b]$](img4.gif) , que vaut la somme de Riemann
associée à
, que vaut la somme de Riemann
associée à 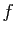 sur
sur 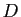 ?
?
- Soit
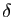 un réel strictement positif.
Quand dit-on de la subdivision pointée
un réel strictement positif.
Quand dit-on de la subdivision pointée 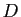 qu'elle est
qu'elle est 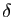 -fine ?
-fine ?
- Soit
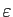 un réel strictement positif.
Quand dit-on que
un réel strictement positif.
Quand dit-on que 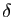 est
est
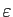 -adapté à
-adapté à 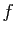 ?
?
Exercice 1 :
Soit 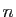 un entier strictement positif.
On rappelle l'expression suivante pour la somme des carrés des
un entier strictement positif.
On rappelle l'expression suivante pour la somme des carrés des 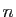 premiers entiers.
premiers entiers.
Soit 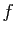 la fonction de
la fonction de
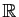 dans
dans
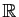 qui à
qui à 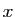 associe
associe 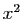 .
On note
.
On note 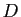 la subdivision
pointée
la subdivision
pointée
![$ D=\{([a_{i-1},a_i],x_i)\}_{1\leqslant i\leqslant n}$](img93.gif) .
.
- Dans cette question, on pose
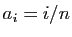 pour tout
pour tout
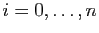 et
et
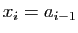 pour
pour
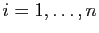 . Montrer que :
. Montrer que :
- Dans cette question, on pose
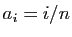 pour tout
pour tout
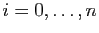 et
et 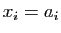 pour
pour
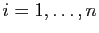 . Montrer que :
. Montrer que :
- Soit
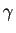 un réel tel que
un réel tel que
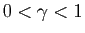 .
Dans cette question, on pose
.
Dans cette question, on pose 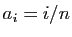 pour tout
pour tout
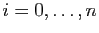 et
et
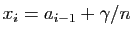 pour
pour
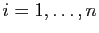 . Montrer que
. Montrer que
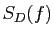 converge vers
converge vers 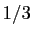 quand
quand 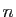 tend vers l'infini.
tend vers l'infini.
- Soient
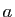 et
et 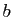 deux réels tels que
deux réels tels que
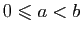 . On
suppose désormais que
. On
suppose désormais que 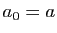 et
et 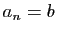 . On pose :
. On pose :
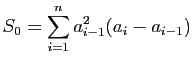
et
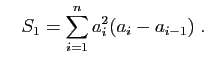
Montrer que
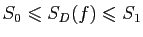 .
.
- On pose :
Montrer que :
- On note
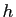 le pas maximal de la subdivision :
le pas maximal de la subdivision :
Montrer que :
- Montrer que
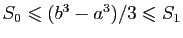 . En déduire que :
. En déduire que :
- En déduire que
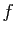 est intégrable sur
est intégrable sur ![$ [a,b]$](img4.gif) et que :
et que :
- Soient
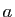 et
et 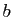 deux réels quelconques.
Montrer que :
deux réels quelconques.
Montrer que :
Exercice 2 :
On dit qu'une fonction de
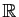 dans
dans
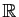 est paire
(respectivement : impaire) si pour
tout réel
est paire
(respectivement : impaire) si pour
tout réel 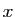 ,
,
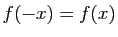 (respectivement :
(respectivement :
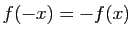 ).
).
- Soit
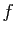 une fonction impaire, admettant une primitive. Montrer que
toute primitive de
une fonction impaire, admettant une primitive. Montrer que
toute primitive de 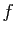 est une fonction paire.
est une fonction paire.
- Soit
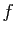 une fonction, admettant une primitive paire. Montrer que pour
tous réels positifs
une fonction, admettant une primitive paire. Montrer que pour
tous réels positifs 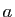 et
et 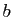 ,
,
- Soit
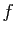 une fonction, admettant une primitive
paire. Déduire de la question précédente que
une fonction, admettant une primitive
paire. Déduire de la question précédente que 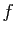 est impaire.
est impaire.
Exercice 3 :
Pour tout
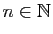 , on pose :
, on pose :
- Calculer
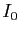 et
et 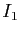 .
.
- En utilisant une intégration par parties, montrer que pour tout
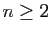 ,
,
En déduire que pour tout 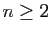 ,
,
- En déduire que pour tout
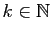 ,
,
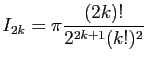
et
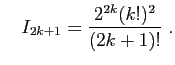
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() de
de
![]() et
intégrable sur
et
intégrable sur ![]() . Soit
. Soit
![]() une subdivision pointée
de
une subdivision pointée
de ![]() .
.
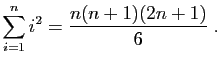
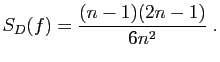
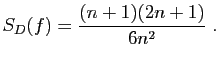
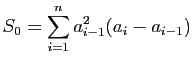 et
et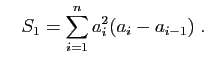
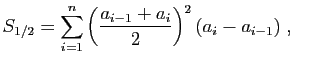
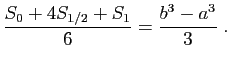
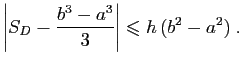
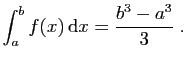
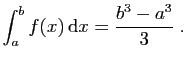
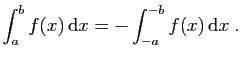
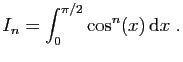
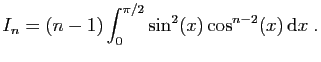
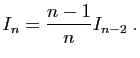
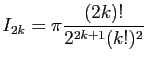 et
et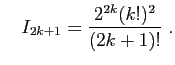
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales