La combinaison de la notion de limite avec les opérations
habituelles sur les suites se passe sans trop de mauvaises
surprises : globalement, les résultats que l'on attend
sont vrais. Nous les énoncerons dans le
théorème 1. Les démonstrations sont
basées sur le lemme suivant.
Lemme 1
- La somme de deux suites convergeant vers 0 converge vers 0.
- Le produit d'une suite convergeant vers 0 par une suite bornée,
converge vers 0.
Démonstration :
- Soient
 et
et 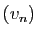 deux suites convergeant vers 0.
Fixons
deux suites convergeant vers 0.
Fixons
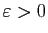 . Soit
. Soit  tel que pour tout
tel que pour tout
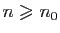 ,
,
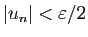 . De même, soit
. De même, soit 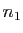 tel que pour tout
tel que pour tout
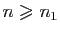 ,
,
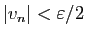 . Alors pour tout
. Alors pour tout
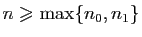 ,
,
d'où le résultat.
- Si la suite
 est bornée, alors il existe
est bornée, alors il existe 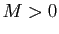 tel que pour
tout entier
tel que pour
tout entier 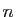 ,
,
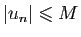 . Soit
. Soit 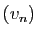 une suite convergeant
vers 0. Fixons
une suite convergeant
vers 0. Fixons
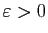 . Soit
. Soit  tel que
pour tout
tel que
pour tout
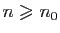 ,
,
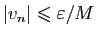 . Pour tout
. Pour tout
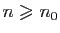 , on a
donc :
, on a
donc :
D'où le résultat.

Théorème 1
- La somme de deux suites convergeant vers une limite finie est
convergente et sa limite est la somme des limites.
- Le produit de deux suites convergeant vers une limite finie est
convergent et sa limite est le produit des limites.
Démonstration : Pour nous ramener au lemme 1, observons d'abord
qu'une suite  a pour limite
a pour limite
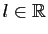 si et seulement si la
suite
si et seulement si la
suite 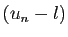 tend vers 0.
tend vers 0.
- Si
 converge vers
converge vers 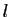 et
et 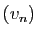 converge vers
converge vers 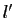 , alors
, alors
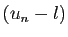 et
et 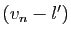 convergent vers 0. Donc
convergent vers 0. Donc
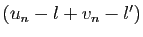 converge vers 0 d'après le point 1. du lemme
1, d'où le résultat.
converge vers 0 d'après le point 1. du lemme
1, d'où le résultat.
- Si
 converge vers
converge vers 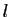 et
et 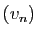 converge vers
converge vers 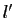 , nous
voulons montrer que
, nous
voulons montrer que
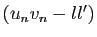 converge vers 0. Ecrivons :
converge vers 0. Ecrivons :
Il suffit donc de montrer séparément que les deux suites
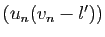 et
et
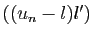 tendent vers 0, d'après le premier
point du lemme 1. Mais chacune de ces deux
suites est le produit d'une suite convergeant vers 0 par une suite
bornée (
tendent vers 0, d'après le premier
point du lemme 1. Mais chacune de ces deux
suites est le produit d'une suite convergeant vers 0 par une suite
bornée ( est bornée car elle est convergente).
D'où le résultat, par le point 2.
du lemme 1.
est bornée car elle est convergente).
D'où le résultat, par le point 2.
du lemme 1.

Le théorème 1 est l'outil de base pour
étudier des convergences de suites à partir des exemples
classiques de la section précédente. On utilise aussi la
composition par une fonction continue. On peut donner deux
définitions équivalentes de la continuité, dont l'une est
parfaitement adaptée aux suites convergentes.
Définition 7
Soit 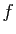 une fonction de
une fonction de
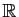 dans
dans
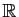 et
et 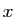 un réel. On dit
que
un réel. On dit
que 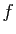 est continue au point
est continue au point 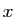 si et seulement si, pour
toute suite
si et seulement si, pour
toute suite  convergeant vers
convergeant vers 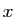 , la suite des images
, la suite des images 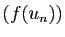 converge vers
converge vers 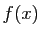 .
.
Toutes les fonctions qui interviennent dans ce cours sont continues en
tout point où elles sont définies, et nous le supposerons pour l'instant.
Par exemple, la fonction
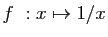 est continue en tout point
de
est continue en tout point
de
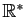 . Donc si une suite
. Donc si une suite  converge vers
converge vers 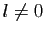 , la
suite des inverses
, la
suite des inverses 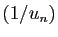 converge vers
converge vers 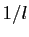 . En utilisant le
théorème 1, on en déduit que le
quotient de deux suites convergentes converge vers le quotient des
limites, pourvu que la limite du dénominateur soit non nulle.
Voici un exemple de calcul de limite, résumant l'ensemble des
techniques que nous avons vues jusqu'ici. Pour tout
. En utilisant le
théorème 1, on en déduit que le
quotient de deux suites convergentes converge vers le quotient des
limites, pourvu que la limite du dénominateur soit non nulle.
Voici un exemple de calcul de limite, résumant l'ensemble des
techniques que nous avons vues jusqu'ici. Pour tout
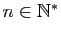 , posons
, posons
Divisons le numérateur et le dénominateur par 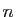 :
:
Les suites
 ,
,
 ,
,
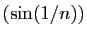 et
et
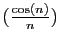 tendent vers 0. On en déduit
que
tendent vers 0. On en déduit
que  tend vers
tend vers 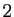 .
Si la limite de
.
Si la limite de  ou celle de
ou celle de 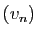 est infinie,
différentes situations peuvent se produire pour la somme
et le produit. Nous les résumons dans les tableaux
1 et 2. Dans ces deux tableaux les
points d'interrogations sont des indéterminations : tous les cas
sont possibles. Par exemple :
est infinie,
différentes situations peuvent se produire pour la somme
et le produit. Nous les résumons dans les tableaux
1 et 2. Dans ces deux tableaux les
points d'interrogations sont des indéterminations : tous les cas
sont possibles. Par exemple :

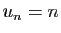 ,
,
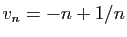 : la suite
: la suite 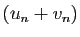 tend vers 0 ;
tend vers 0 ;

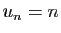 ,
, 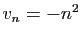 : la suite
: la suite 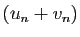 tend vers
tend vers 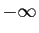 ;
;

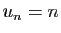 ,
,
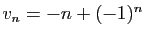 : la suite
: la suite 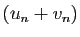 ne converge pas.
ne converge pas.
Tableau 1:
Limites possibles de 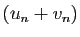 en fonction des limites de
en fonction des limites de
 et
et 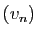 .
.
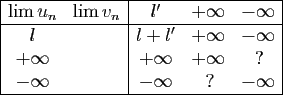 |
Tableau 2:
Limites possibles de 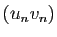 en fonction des limites de
en fonction des limites de
 et
et 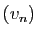 .
.
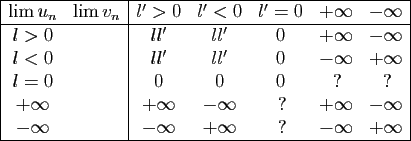 |
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
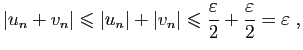
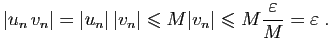
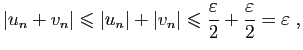
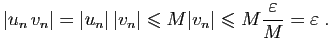
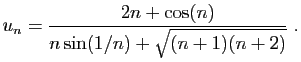
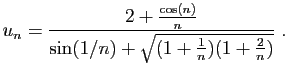
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales