On dit que la suite  converge vers un réel
converge vers un réel 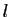 (sa
limite) si tout intervalle ouvert contenant
(sa
limite) si tout intervalle ouvert contenant 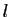 , contient aussi tous les
, contient aussi tous les
 pour
pour 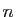 assez grand.
assez grand.
Autrement dit, tout intervalle ouvert centré en 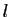 contient tous les
termes de la suite à partir d'un certain rang. Observons que le rang
contient tous les
termes de la suite à partir d'un certain rang. Observons que le rang
 à partir duquel tous les termes de la suite restent dans
l'intervalle
à partir duquel tous les termes de la suite restent dans
l'intervalle
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) , dépend de
, dépend de
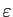 .
La figure 1 représente les
.
La figure 1 représente les 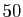 premiers termes
de la suite
premiers termes
de la suite
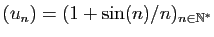 . La limite est
. La limite est 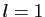 . On a :
. On a :
Fixons
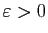 (sur la figure
(sur la figure
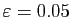 ). Posons
). Posons
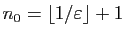 (
(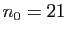 pour
pour
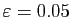 ).
Pour tout
).
Pour tout
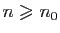 ,
,
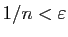 , donc
, donc
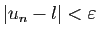 .
Sur la figure 1, on constate en fait que
.
Sur la figure 1, on constate en fait que
![$ u_n\in [0.95,1.05]$](img96.gif) pour
pour
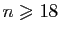 .
.
Figure:
Convergence de la suite
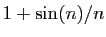 .
.
|
|
On étend la notion de convergence aux limites infinies de la façon
suivante.
Définition 6
Soit  une suite de réels.
une suite de réels.
- On dit que
 tend vers
tend vers 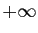 si
si
- On dit que
 tend vers
tend vers 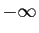 si
si
Il est commode de pouvoir dire qu'une suite «tend vers l'infini»,
mais cela induit une certaine ambiguïté sur la notion de
convergence.
De même qu'il faut voir
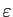 comme un «petit» réel (proche de
0), dans la définition 6 il faut comprendre
comme un «petit» réel (proche de
0), dans la définition 6 il faut comprendre 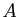 comme
grand (proche de l'infini). Une suite tend vers
comme
grand (proche de l'infini). Une suite tend vers 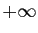 si ses termes
restent au-dessus de n'importe quelle quantité, à partir d'un
certain rang.
Voici quelques exemples classiques.
si ses termes
restent au-dessus de n'importe quelle quantité, à partir d'un
certain rang.
Voici quelques exemples classiques.

- Suites arithmétiques :
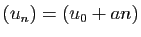
- Si
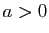 ,
,  tend vers
tend vers 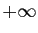 .
.
- Si
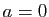 ,
,  est constante (tend vers
est constante (tend vers 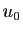 ).
).
- Si
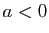 ,
,  tend vers
tend vers 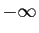 .
.

- Suites géométriques :
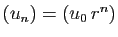
- Si
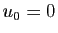 ,
,  est constante (tend vers 0).
est constante (tend vers 0).
- Si
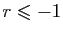 , et
, et 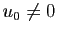 ,
,  ne converge pas.
ne converge pas.
- Si
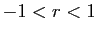 ,
,  tend vers 0.
tend vers 0.
- Si
 ,
,  est constante (tend vers
est constante (tend vers 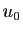 ).
).
- Si
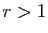 et
et 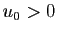 ,
,  tend vers
tend vers 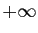 .
.
- Si
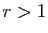 et
et 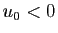 ,
,  tend vers
tend vers 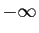 .
.

- Suites de Riemann :
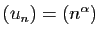
- Si
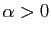 ,
,  tend vers
tend vers 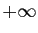 .
.
- Si
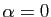 ,
,  est constante (tend vers
est constante (tend vers 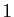 ).
).
- Si
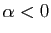 ,
,  tend vers 0.
tend vers 0.
Pour bien comprendre la notion de convergence, nous allons en
étudier quelques conséquences faciles, rassemblées dans la
proposition suivante.
Proposition 1
Soit  une suite de réels :
une suite de réels :
- si
 converge, alors sa limite est unique ;
converge, alors sa limite est unique ;
- si
 converge vers une limite finie, alors
converge vers une limite finie, alors  est bornée ;
est bornée ;
- si pour tout
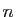 ,
,
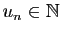 et si
et si  converge vers une limite
finie, alors
converge vers une limite
finie, alors  est
constante à partir d'un certain rang ;
est
constante à partir d'un certain rang ;
- si
 converge vers
converge vers 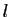 ,
alors toute suite extraite de
,
alors toute suite extraite de  converge vers
converge vers 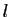 ;
;
- si les deux suites extraites
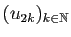 et
et
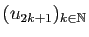 convergent
vers la même limite
convergent
vers la même limite 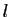 (finie ou infinie), alors
(finie ou infinie), alors
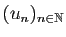 converge vers
converge vers 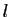 .
.
Démonstration : Les démonstrations des 5 points se ressemblent.
- Supposons que
 vérifie la définition 5
pour deux réels
vérifie la définition 5
pour deux réels 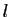 et
et 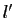 distincts. Posons
distincts. Posons
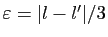 . Alors
les intervalles
. Alors
les intervalles
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) et
et
![$ [l'-\varepsilon ,l'+\varepsilon ]$](img128.gif) sont
disjoints. À partir d'un certain rang, les
sont
disjoints. À partir d'un certain rang, les  devraient appartenir
aux deux à la fois : c'est impossible.
devraient appartenir
aux deux à la fois : c'est impossible.
- Fixons
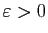 , et
, et  tel que
tel que  reste dans l'intervalle
reste dans l'intervalle
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) pour tout
pour tout
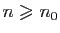 . Alors :
. Alors :
et
- Soit
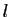 la limite. Si
la limite. Si 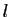 n'était pas un entier,
pour
n'était pas un entier,
pour
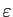 suffisamment petit, l'intervalle
suffisamment petit, l'intervalle
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) ne
contiendrait aucun entier, donc aucun des
ne
contiendrait aucun entier, donc aucun des  .
Donc
.
Donc 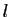 doit être un entier. Posons
doit être un entier. Posons
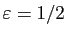 . L'intervalle
. L'intervalle
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) ne contient qu'un seul
entier,
ne contient qu'un seul
entier, 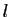 . Comme à partir d'un certain rang tous les
. Comme à partir d'un certain rang tous les  sont
dans cet intervalle, et qu'ils sont tous entiers, ils sont tous
égaux à
sont
dans cet intervalle, et qu'ils sont tous entiers, ils sont tous
égaux à 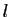 .
.
- Soit
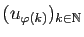 une suite extraite de
une suite extraite de
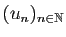 . Comme
. Comme 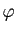 est strictement croissante, pour
tout
est strictement croissante, pour
tout  il existe
il existe 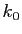 tel que
tel que
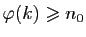 pour tout
pour tout
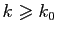 . Si tous les
. Si tous les  sont dans l'intervalle
sont dans l'intervalle
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) à partir du rang
à partir du rang  , tous les
, tous les
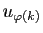 sont dans le même intervalle à partir du rang
sont dans le même intervalle à partir du rang 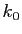 .
.
- Fixons
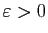 . Soit
. Soit 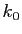 tel que
tel que 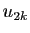 reste dans
l'intervalle
reste dans
l'intervalle
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) pour tout
pour tout
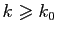 .
Soit
.
Soit 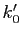 tel que
tel que 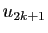 reste dans
l'intervalle
reste dans
l'intervalle
![$ [l-\varepsilon ,l+\varepsilon ]$](img84.gif) pour tout
pour tout
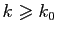 .
Alors pour tout
.
Alors pour tout
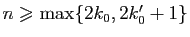 ,
,
![$ u_n\in [l-\varepsilon ,l+\varepsilon ]$](img141.gif) .
La démonstration pour une limite infinie est analogue.
.
La démonstration pour une limite infinie est analogue.

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() converge vers un réel
converge vers un réel ![]() (sa
limite) si tout intervalle ouvert contenant
(sa
limite) si tout intervalle ouvert contenant ![]() , contient aussi tous les
, contient aussi tous les
![]() pour
pour ![]() assez grand.
assez grand.
![]() comme un «petit» réel (proche de
0), dans la définition 6 il faut comprendre
comme un «petit» réel (proche de
0), dans la définition 6 il faut comprendre ![]() comme
grand (proche de l'infini). Une suite tend vers
comme
grand (proche de l'infini). Une suite tend vers ![]() si ses termes
restent au-dessus de n'importe quelle quantité, à partir d'un
certain rang.
Voici quelques exemples classiques.
si ses termes
restent au-dessus de n'importe quelle quantité, à partir d'un
certain rang.
Voici quelques exemples classiques.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales