Définition 1
Soit 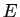 un ensemble. On appelle suite à valeurs dans
un ensemble. On appelle suite à valeurs dans 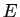 une
application de
une
application de
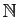 dans
dans 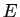 . L'ensemble des suites à valeurs dans
. L'ensemble des suites à valeurs dans
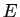 est noté
est noté
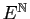 .
.
Dans ce chapitre, nous nous préoccuperons surtout des suites à
valeurs dans
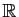 (nous dirons aussi suites de réels)
et très peu des suites à valeurs dans
(nous dirons aussi suites de réels)
et très peu des suites à valeurs dans
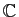 (suites de complexes).
Une suite à valeurs dans
(suites de complexes).
Une suite à valeurs dans
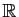 sera typiquement
notée
sera typiquement
notée
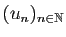 ou simplement
ou simplement  quand il n'y a pas
d'ambiguïté. Les entiers
quand il n'y a pas
d'ambiguïté. Les entiers 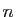 sont les indices de la suite
et leurs images
sont les indices de la suite
et leurs images  sont les termes de la suite.
La suite
sont les termes de la suite.
La suite
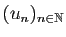 est un objet différent de l'ensemble
est un objet différent de l'ensemble
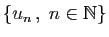 . En particulier une suite aura toujours une
infinité de termes, même si ces termes ne prennent qu'un nombre fini
de valeurs différentes. Par exemple, pour
. En particulier une suite aura toujours une
infinité de termes, même si ces termes ne prennent qu'un nombre fini
de valeurs différentes. Par exemple, pour
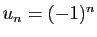 ,
la suite est
,
la suite est
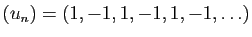 , et l'ensemble
, et l'ensemble
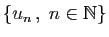 est l'ensemble
est l'ensemble 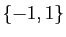 .
Il existe deux manières de définir une suite de réels à partir d'une
fonction :
.
Il existe deux manières de définir une suite de réels à partir d'une
fonction :

- définition explicite :
où
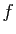 est une fonction de
est une fonction de
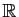 dans
dans
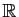 . Par exemple :
. Par exemple :
-
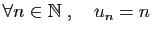
-
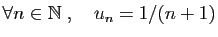
-
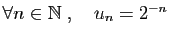 .
.

- définition par récurrence :
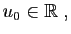
et
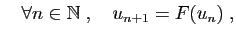
où 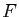 est une fonction de
est une fonction de
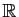 dans
dans
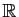 . Les mêmes exemples peuvent
être définis par :
. Les mêmes exemples peuvent
être définis par :
-
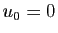 et
et 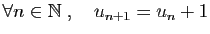
-
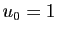 et
et 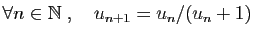
-
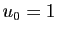 et
et 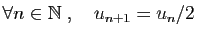 .
.
Voici deux exemples génériques.
Définition 2
- Soit
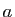 un réel.
On appelle suite arithmétique de raison
un réel.
On appelle suite arithmétique de raison 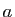 une suite
définie par
une suite
définie par
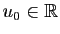 et
et
- Soit
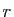 un réel.
On appelle suite géométrique de raison
un réel.
On appelle suite géométrique de raison 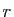 une suite
définie par
une suite
définie par
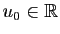 et
et
On vérifie facilement par récurrence qu'une suite arithmétique
de raison 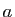 a pour terme général
a pour terme général
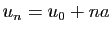 . De même, une
suite géométrique de raison
. De même, une
suite géométrique de raison 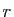 a pour terme général
a pour terme général
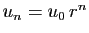 .
.
Définition 3
Soit
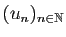 une suite de réels. On dit que la
suite
une suite de réels. On dit que la
suite  est :
est :

- constante si
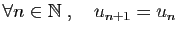 ;
;

- croissante si
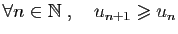 ;
;

- décroissante si
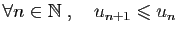 ;
;

- strictement croissante si
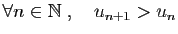 ;
;

- strictement décroissante si
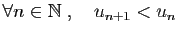 ;
;

- monotone si elle est croissante ou décroissante

- majorée si
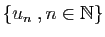 est majoré ;
est majoré ;

- minorée si
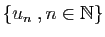 est minoré ;
est minoré ;

- bornée si
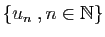 est borné ;
est borné ;

- périodique si
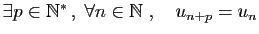 .
.
Il arrive qu'une suite ne soit définie que sur
une partie de
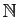 : par exemple
: par exemple
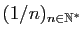 . On sera
également amené à réduire la suite aux indices au-delà d'un
certain entier
. On sera
également amené à réduire la suite aux indices au-delà d'un
certain entier  :
:
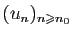 .
L'expression «à partir d'un certain rang» reviendra souvent dans
ce qui suit. Dire que la suite
.
L'expression «à partir d'un certain rang» reviendra souvent dans
ce qui suit. Dire que la suite
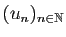 possède la
propriété
possède la
propriété 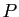 à partir d'un certain rang signifie que la
suite
à partir d'un certain rang signifie que la
suite
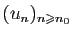 la possède pour un certain
la possède pour un certain  . On dit
aussi «
. On dit
aussi «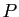 est vraie pour
est vraie pour 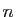 assez grand». Voici
quelques exemples.
assez grand». Voici
quelques exemples.
Définition 4
Soit
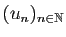 une suite de réels. On dit que la
suite
une suite de réels. On dit que la
suite  est
est

- constante à partir d'un certain rang (on dit aussi stationnaire) si
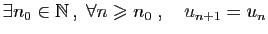 ;
;

- croissante à partir d'un certain rang si
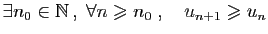 ;
;

- périodique à partir d'un certain rang si
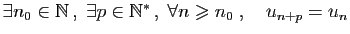 ;
;
Par exemple, la suite
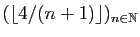 est constante à partir du rang
est constante à partir du rang 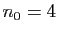 .
La suite des décimales de
.
La suite des décimales de 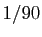 est constante à partir
du rang
est constante à partir
du rang 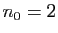 . La suite
. La suite
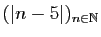 est croissante
à partir du rang
est croissante
à partir du rang 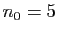 . La suite des décimales de
. La suite des décimales de
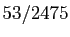 est périodique, de
période
est périodique, de
période 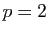 à partir
du rang
à partir
du rang 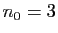 . Quel que soit le nombre rationnel
. Quel que soit le nombre rationnel 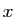 , la suite des
décimales de
, la suite des
décimales de 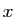 est périodique à partir d'un certain rang.
est périodique à partir d'un certain rang.
Si la suite
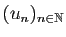 est «majorée à partir d'un certain
rang», alors elle est majorée tout court. En effet si
est «majorée à partir d'un certain
rang», alors elle est majorée tout court. En effet si
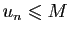 pour tout
pour tout
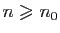 ,
alors pour tout entier
,
alors pour tout entier
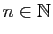 ,
,
De même une suite minorée à
partir d'un certain rang est minorée, une suite bornée à partir
d'un certain rang est bornée.
Les opérations sur les réels s'étendent aux suites en des
opérations terme à terme.

- addition :
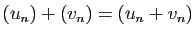 ,
,

- multiplication :
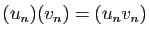 ,
,

- multiplication par un réel :
 ,
,

- comparaison :
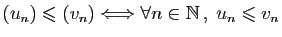 .
.
L'addition a les mêmes propriétés que celle des réels :
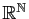 muni de l'addition est un groupe commutatif.
Muni de l'addition et de la multiplication
par un réel, c'est un espace vectoriel.
Cependant, le produit de deux suites peut être
nul sans que les deux suites le soient :
muni de l'addition est un groupe commutatif.
Muni de l'addition et de la multiplication
par un réel, c'est un espace vectoriel.
Cependant, le produit de deux suites peut être
nul sans que les deux suites le soient :
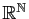 muni de l'addition et de la
mutiplication est un anneau commutatif non intègre.
Etant donnée une suite
muni de l'addition et de la
mutiplication est un anneau commutatif non intègre.
Etant donnée une suite  , on appelle suite extraite ou
sous-suite, une
suite formée de certains termes de
, on appelle suite extraite ou
sous-suite, une
suite formée de certains termes de  , c'est-à-dire une suite
de la forme
, c'est-à-dire une suite
de la forme
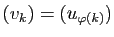 , où
, où 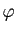 est une application
strictement croissante de
est une application
strictement croissante de
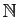 dans
dans
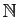 . Par exemple si
. Par exemple si  est
la suite géométrique
est
la suite géométrique
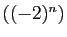 , et
, et
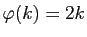 , alors
, alors
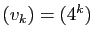 : on a extrait de la suite
: on a extrait de la suite  la suite des termes
d'indice pair.
la suite des termes
d'indice pair.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() est «majorée à partir d'un certain
rang», alors elle est majorée tout court. En effet si
est «majorée à partir d'un certain
rang», alors elle est majorée tout court. En effet si
![]() pour tout
pour tout
![]() ,
alors pour tout entier
,
alors pour tout entier
![]() ,
,
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales