-
- La suite
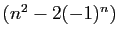 est croissante à partir d'un certain rang.
est croissante à partir d'un certain rang.
-
- La suite
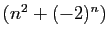 est croissante à partir d'un certain rang.
est croissante à partir d'un certain rang.
-
- La suite
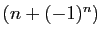 est croissante à partir d'un certain rang.
est croissante à partir d'un certain rang.
-
- La suite
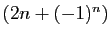 est croissante.
est croissante.
-
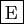
- La suite
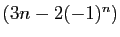 est croissante à partir d'un certain rang.
est croissante à partir d'un certain rang.
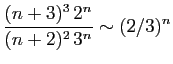
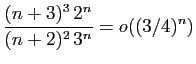
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales