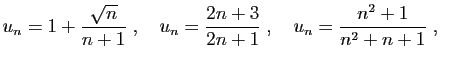
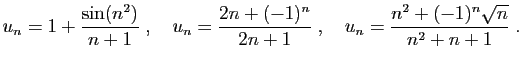
- Montrer qu'elle converge vers
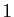 .
.
- Pour
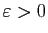 fixé, déterminer en fonction de
fixé, déterminer en fonction de
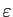 le rang
le rang  à partir duquel tous les termes de la suite restent dans
l'intervalle
à partir duquel tous les termes de la suite restent dans
l'intervalle
![$ [1-\varepsilon ,1+\varepsilon ]$](img428.gif) .
.
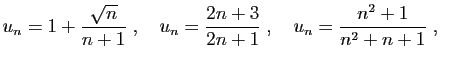
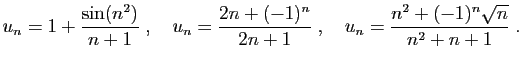
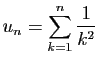 et
et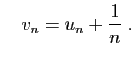
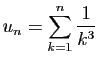 et
et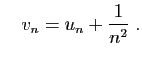
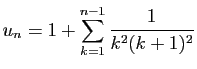 et
et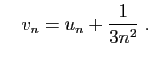
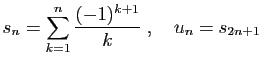 et
et
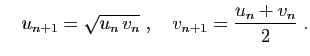
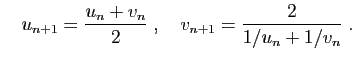
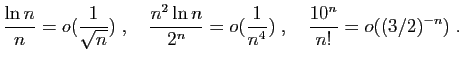
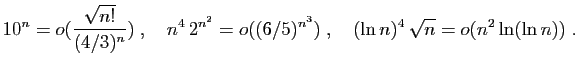
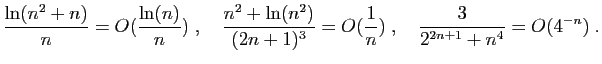
![$\displaystyle \frac{2n+\sqrt{n}}{\sqrt[3]{2n+3}}=O(n^{2/3})\;,\quad
\ln(n^2+2n+3)=O(\ln(n))\;,\quad
\frac{4n^2+3n\cos(n)}{5n-\sin(n+3)}= O(n)\;.
$](img448.gif)
![$\displaystyle \frac{4n^3-\sqrt{n^5+3n^4}}{(\sqrt{2}n+\sqrt{n})^4}\sim\frac{1}{n...
...\;,\quad
\frac{\sqrt[3]{n^2+2n\cos(n)}}{\sqrt{n^3+n^2\sin(n)}}\sim n^{-5/6}\;.
$](img449.gif)
![$\displaystyle \frac{2n+\ln(n^3)}{\sqrt{4n+5}}\sim \sqrt{n}\;,\quad
\frac{\ln(2^...
...n}\;,\quad
\frac{\sqrt[3]{n^2+2n\cos(n)}}{\sqrt{n+\sin(n)}}\sim \sqrt[6]{n}\;.
$](img450.gif)
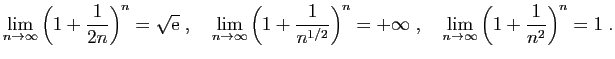
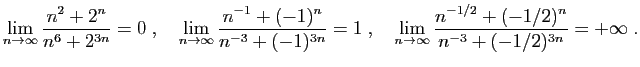
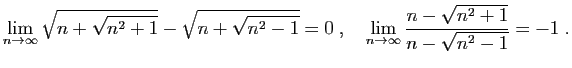
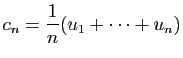
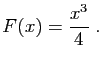
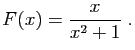
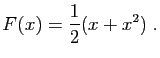
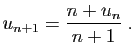
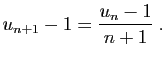
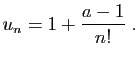
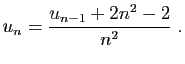
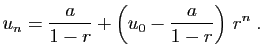
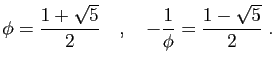
![\begin{displaymath}
\left\{
\begin{array}{lcl}
a+b&=&1\ [1.5ex]
a\phi-b/\phi&=&1
\end{array}\right.
\end{displaymath}](img512.gif)
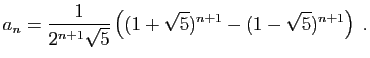
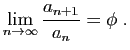
![\begin{displaymath}
\left\{
\begin{array}{lcl}
a_{n+1}&=&(a_n-b_n)/2\ [1.5ex]
b_{n+1}&=&(a_n+b_n)/2\;.
\end{array}\right.
\end{displaymath}](img517.gif)
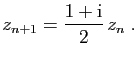
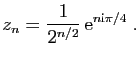
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales