 Si
Si 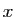 est rationnel, la suite des décimales de
est rationnel, la suite des décimales de 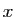 est
périodique.
est
périodique.
-
 Si
Si 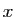 est décimal, la suite des décimales de
est décimal, la suite des décimales de 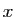 est constante
à partir d'un certain rang.
est constante
à partir d'un certain rang.
-
 Toute suite récurrente qui ne prend qu'un nombre fini de valeurs
distinctes, est périodique à partir d'un certain rang.
Toute suite récurrente qui ne prend qu'un nombre fini de valeurs
distinctes, est périodique à partir d'un certain rang.
 Si
Si 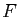 est une application croissante,
la suite
est une application croissante,
la suite
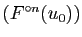 est croissante.
est croissante.
-
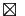 Si
Si 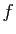 est une application croissante, la suite
est une application croissante, la suite 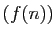 est croissante.
est croissante.
-
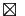 Si
Si 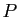 est une application polynôme, la suite
est une application polynôme, la suite 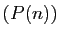 est monotone
à partir d'un certain rang.
est monotone
à partir d'un certain rang.
 La suite
La suite
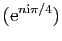 est périodique de période
est périodique de période 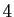 .
.
-
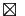 La suite
La suite 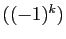 est une suite extraite de la suite
est une suite extraite de la suite
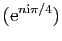 .
.
-
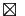 On peut extraire de la suite
On peut extraire de la suite
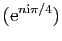 une sous-suite constante.
une sous-suite constante.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales