Une série est dite convergente si ses termes forment une suite décroissante vers 0.La série harmonique
Assez notable est la controverse sur la sérieLa controverse en question avait débuté en 1703 avec un travail de Guido Grandi (1671-1742) sur la quadrature du cercle (un de plus). Quand Grandi évoque la série alternéedont la somme a été donnée par Leibniz comme étant
, bien que d'autres ne soient pas d'accord. Personne n'a encore assigné de valeur à cette somme, et donc la controverse porte sur la question de savoir si les séries de ce type ont une somme. La compréhension de cette question réside dans le mot «somme» ; cette idée, si on la conçoit ainsi -la somme d'une série est la quantité dont on s'approche d'autant plus qu'on ajoute plus de termes- ne vaut que pour les séries convergentes, et nous devrions en général abandonner cette idée pour des sommes de séries divergentes.
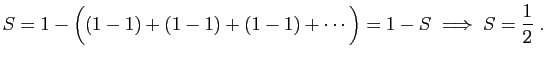
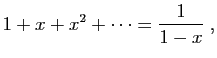
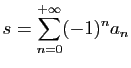
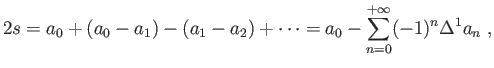
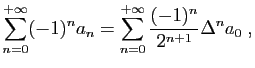
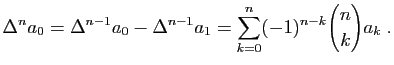
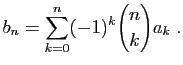
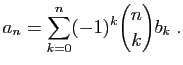
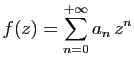
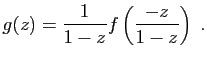
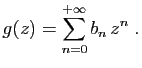
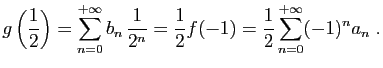
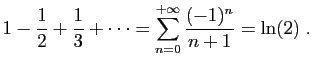
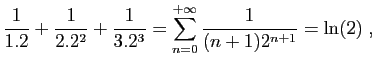
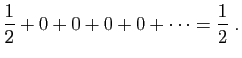
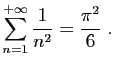
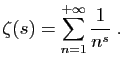
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales