Vous avez le choix !

Prenez une série $\sum u_n$ convergente, mais non absolument convergente, par exemple $\sum (-1)^n/n$. Nous vous avons fait démontrer en exercice qu'on peut en permutant les termes, obtenir n'importe quelle somme, y compris $\pm \infty$. Vous pouvez préférer que ce soit Cauchy qui vous le dise⁶.

Si les différents termes de la série proposée étaient les uns positifs, les autres négatifs, il pourrait arriver que la série fût convergente, et que les termes dans lesquels la somme des indices serait au moins égale à $n$, étant ajoutés les uns aux autres dans un certain ordre, ne donnassent pas toujours une somme infiniment petite pour des valeurs infiniment grandes de $n$. Cette remarque est applicable même aux séries simples. Ainsi, en particulier, si l'on considère la série simple

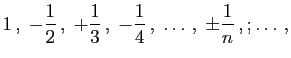$$1 ,\;-\frac{1}{2} ,\;+\frac{1}{3} ,\;-\frac{1}{4} ,\;\ldots ,\; \pm \frac{1}{n} ,; \ldots ,$$ (6)

[...] on peut affirmer que la somme $s_n$ convergera pour des valeurs croissantes de $n$ vers une limite fixe $s$ et que la série (6) sera convergente. Mais si au lieu d'ajouter les uns aux autres les termes [...] pris dans l'ordre où ils se trouvent, on venait à intervertir cet ordre en choisissant parmi eux des termes affectés du même signe, par exemple les suivants

$$\pm\frac{1}{n+2} ,\;\pm\frac{1}{n+4} ,\;\ldots ,\; \pm\frac{1}{n+2n}=\pm\frac{1}{3n} ,$$

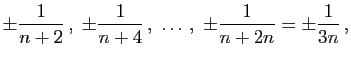
la valeur numérique de la somme de ces derniers termes, savoir

$$\frac{1}{n+2}+\frac{1}{n+4}+\ldots+\frac{1}{3n}$$

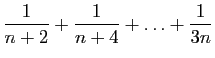
surpasserait évidemment le produit

$$n\times \frac{1}{3n}$$

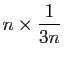
et cesserait d'être infiniment petite pour des valeurs infiniment grandes de $n$.

Par contre, pour une série absolument convergente, on peut permuter les termes comme on veut sans modifier ni la convergence absolue, ni la somme (on dit que la série est commutativement convergente). Voici le résultat, énoncé par un autre mathématicien du XIX^e, beaucoup moins prestigieux mais peut être un tantinet plus pédagogue, Charles Cellérier (1818-1889)⁷.

Observons que, si une série convergente a tous ses termes positifs, on peut à volonté changer leur ordre, en réunir plusieurs en un seul, ou réciproquement remplacer un seul par d'autres tous positifs, dont il est la somme ; on peut aussi mettre à part des termes en nombre infini, la somme des deux séries formées soit par ceux-là, soit par ceux qui restent, reproduit la primitive. Convenons, pour abréger, de dire qu'une série est numériquement convergente lorsqu'elle a des termes positifs et négatifs, mais reste convergente en les prenant tous avec le signe $+$. Dans ce cas également, on peut changer à volonté l'ordre des termes, remplacer quelques-uns d'entre eux, même en nombre infini, par un seul égal à leur somme, et en répétant l'opération, remplacer la série primitive par une autre dont les termes soient eux-mêmes des séries. Il suffit que tout terme choisi à volonté dans l'ordre ancien ait sa place déterminée dans l'ordre nouveau.