-
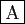
- Si la suite
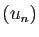 tend vers 0, alors la série
tend vers 0, alors la série
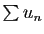 converge.
converge.
-
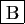
- Si la série
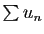 diverge, alors la série
diverge, alors la série
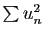 diverge.
diverge.
-
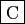
- Si la série
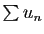 diverge, alors la suite
diverge, alors la suite 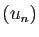 ne tend pas
vers 0.
ne tend pas
vers 0.
-
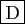
- Si la série
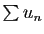 converge, alors la suite
converge, alors la suite 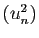 tend vers 0.
tend vers 0.
-
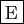
- Si la série
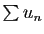 converge, alors la série
converge, alors la série
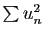 converge.
converge.
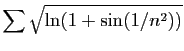
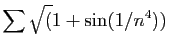
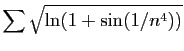
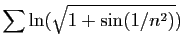
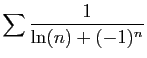
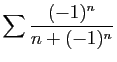
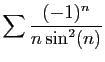
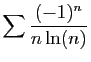
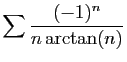
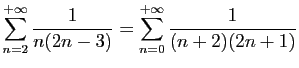
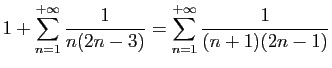
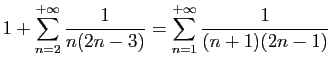
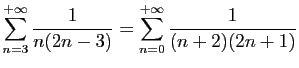
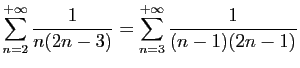
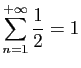
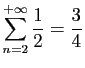
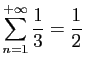
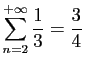
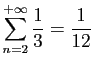
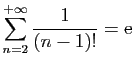
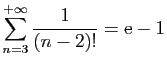
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales