Une fois le système mis sous forme échelonnée, s'il y a des
équations de compatibilité et si l'un des
seconds membres de ces équations est non nul, le système n'a pas
de solution (on dit qu'il est impossible). C'est le cas par exemple
pour le système 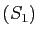 de la section précédente.
de la section précédente.
S'il n'y a pas d'équations de compatibilité ou si leurs seconds
membres sont nuls, le système a des solutions et il faut les
calculer. À partir du système échelonné 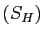 ,
les étapes successives sont les suivantes.
,
les étapes successives sont les suivantes.
- supprimer les équations de compatibilité s'il y en a,
- diviser chacune des équations restantes par son pivot,
- si
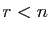 , passer les termes en
, passer les termes en
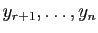 dans le second membre,
dans le second membre,
- calculer
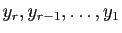 , par combinaisons de lignes,
en annulant les termes au-dessus de chaque
pivot et en commençant par le dernier. Si
, par combinaisons de lignes,
en annulant les termes au-dessus de chaque
pivot et en commençant par le dernier. Si 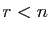 ,
,
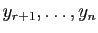 sont traités comme des paramètres, qui
peuvent prendre des valeurs réelles arbitraires.
sont traités comme des paramètres, qui
peuvent prendre des valeurs réelles arbitraires.
Nous reprenons comme exemples les systèmes 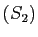 et
et 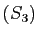 de la
section précédente.
de la
section précédente.
Le système est maintenant sous forme résolue :
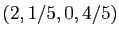 est
la seule solution.
Voici un autre exemple.
est
la seule solution.
Voici un autre exemple.
Le système est maintenant sous forme résolue. Il admet une infinité de
solutions, dépendant du paramètre 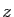 . L'ensemble
. L'ensemble 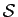 des
solutions s'écrit
des
solutions s'écrit
C'est bien la forme prévue par le théorème 2 : 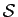 est
une droite affine, passant par la solution particulière
est
une droite affine, passant par la solution particulière
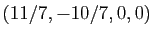 , de vecteur directeur
, de vecteur directeur
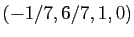 . Evidemment l'écriture de l'ensemble des solutions
obtenue pas la méthode de Gauss, n'est pas la seule possible.
Dans l'exemple ci-dessus,
. Evidemment l'écriture de l'ensemble des solutions
obtenue pas la méthode de Gauss, n'est pas la seule possible.
Dans l'exemple ci-dessus, 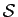 pourrait aussi s'écrire :
pourrait aussi s'écrire :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() ,
les étapes successives sont les suivantes.
,
les étapes successives sont les suivantes.
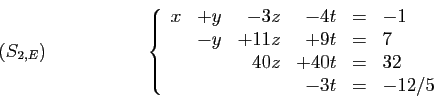
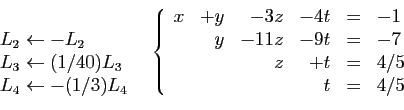
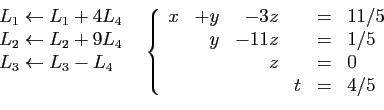
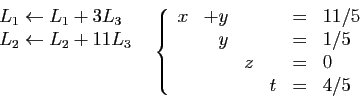
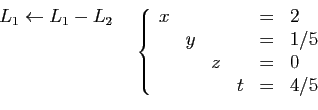
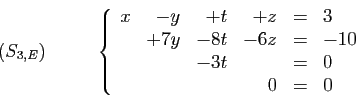
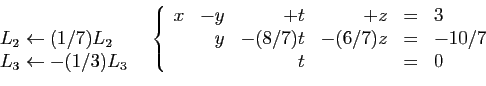
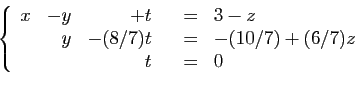
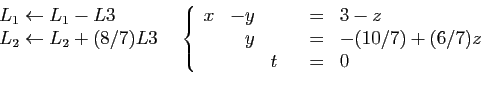
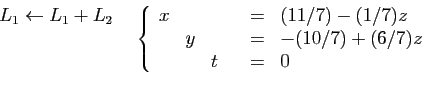
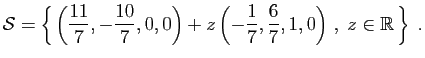
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales