L'idée de la méthode de Gauss est de transformer par étapes,
le système à résoudre
en des systèmes plus simples, tous équivalents au
système initial, jusqu'à un système dit
«résolu», sur lequel on lit directement la solution.
Pour un système
linéaire, «plus simple» signifie «avec moins de termes»,
ou encore «plus de coefficients nuls» . Pour annuler des termes,
la méthode de Gauss combine les trois transformations de la
proposition suivante.
Proposition 1
Les transformations suivantes changent tout système
en un système équivalent :
- échanger deux lignes,
- multiplier une ligne par un réel non nul,
- ajouter une ligne à une autre ligne.
Démonstration : Le résultat est évident pour la première transformation. Pour la
seconde, si
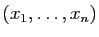 est solution de
est solution de 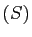 , contenant
l'équation
, contenant
l'équation
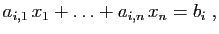 |
(3) |
alors
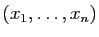 vérifie encore
vérifie encore
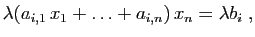 |
(4) |
pour tout 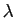 . Réciproquement, si
. Réciproquement, si 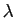 est non nul il
suffit d'appliquer ce qui précède à
est non nul il
suffit d'appliquer ce qui précède à 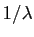 pour s'assurer
que tout
pour s'assurer
que tout 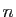 -uplet solution de (4) est aussi solution de
(3).
-uplet solution de (4) est aussi solution de
(3).
Pour le point 3, considérons les deux lignes
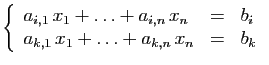 |
(5) |
Elles sont remplacées par
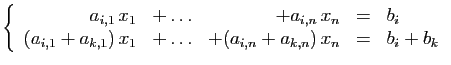 |
(6) |
Si un 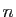 -uplet
-uplet
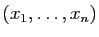 vérifie (5), alors il
vérifie aussi (6). Réciproquement, multiplions la
première équation de (6) par
vérifie (5), alors il
vérifie aussi (6). Réciproquement, multiplions la
première équation de (6) par 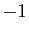 (ce qui ne change pas
l'ensemble des solutions d'après le point 2), puis ajoutons
les deux équations. D'après ce qui précède, toute solution de
(6) est aussi solution de (5).
(ce qui ne change pas
l'ensemble des solutions d'après le point 2), puis ajoutons
les deux équations. D'après ce qui précède, toute solution de
(6) est aussi solution de (5).
Ici, une mise en garde s'impose. Lorsqu'on remplace une ligne par une
combinaison linéaire des autres, toute solution du système
initial est encore solution du nouveau système. Mais l'ensemble des
solutions du nouveau peut être strictement plus grand.
Dans la démonstration ci-dessus, nous avons pris soin de
vérifier les réciproques : il est essentiel que le système
transformé soit bien équivalent au système initial.
La méthode de Gauss consiste à appliquer successivement les
transformations de la proposition 1. Dans les
deux sections suivantes, nous allons décrire les deux étapes
principales.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales