Une équation linéaire à deux inconnues, du type
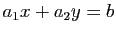 ,
est l'équation d'une droite dans le plan. Plus précisément, si
,
est l'équation d'une droite dans le plan. Plus précisément, si
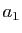 ,
, 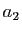 et
et 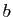 sont des réels fixés, tels que
sont des réels fixés, tels que 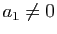 ou
ou
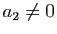 , l'ensemble des couples
, l'ensemble des couples 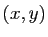 vérifiant
vérifiant
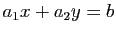 est
une droite affine.
Chercher les couples
est
une droite affine.
Chercher les couples 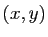 qui vérifient plusieurs
équations du même type, c'est chercher les points communs à
plusieurs droites affines. Voici
trois exemples de systèmes de 3 équations à 2 inconnues.
qui vérifient plusieurs
équations du même type, c'est chercher les points communs à
plusieurs droites affines. Voici
trois exemples de systèmes de 3 équations à 2 inconnues.
Le premier n'a pas de solution. Le
second a une solution unique : la solution de ses deux premières
équations vérifie la troisième. Le troisième système
a une infinité de solutions : ses trois équations sont équivalentes.
La figure 1 donne une interprétation géométrique
des trois systèmes. Dans chacun des trois graphiques,
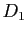 ,
, 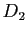 ,
, 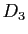 sont les droites correspondant aux trois
équations du système.
sont les droites correspondant aux trois
équations du système.
Figure 1:
Interprétations géométriques de 3 systèmes
linéaires de 3 équations à 2 inconnues.
|
|
Résoudre un système de 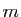 équations à 2 inconnues, c'est
déterminer l'intersection de
équations à 2 inconnues, c'est
déterminer l'intersection de 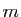 droites dans le
plan. Elle peut être vide, réduite à un point, ou égale à une
droite.
Une équation linéaire à trois inconnues
droites dans le
plan. Elle peut être vide, réduite à un point, ou égale à une
droite.
Une équation linéaire à trois inconnues 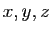 est l'équation
d'un plan dans l'espace. Voici trois systèmes de deux équations
à trois inconnues.
est l'équation
d'un plan dans l'espace. Voici trois systèmes de deux équations
à trois inconnues.
Les deux équations du premier système représentent le même
plan. L'ensemble des solutions du système est ce plan. Dans le second
système, les équations sont celles de deux plans
parallèles : leur intersection est vide. Le troisième système
est le cas général : l'intersection des deux plans
est une droite. Les trois cas sont illustrés par la figure
2.
Figure 2:
Interprétations géométriques de 3 systèmes
linéaires de 2 équations à 3 inconnues.
|
|
Un système de 3 équations à 3
inconnues peut avoir une solution unique (l'intersection de trois
plans «en position générale»
est un point de l'espace). Mais il peut se
faire que deux des plans soient parallèles, auquel cas le système
n'aura pas de solution, ou bien que l'un des plans contienne
l'intersection des deux autres, auquel cas le système aura une
infinité de solutions.
Un système linéaire
de 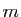 équations à
équations à 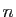 inconnues se présente sous
la forme suivante.
inconnues se présente sous
la forme suivante.
Une solution de 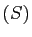 est un
est un 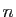 -uplet de réels qui satisfont
à la fois ses
-uplet de réels qui satisfont
à la fois ses 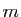 équations. Résoudre le système
équations. Résoudre le système 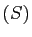 c'est décrire l'ensemble des solutions.
L'intuition géométrique des dimensions 2 et 3 reste valable en
dimension
c'est décrire l'ensemble des solutions.
L'intuition géométrique des dimensions 2 et 3 reste valable en
dimension 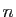 : l'ensemble des
: l'ensemble des 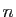 -uplets de réels
-uplets de réels
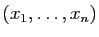 qui vérifient une équation du type
qui vérifient une équation du type
où les 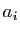 sont non tous nuls,
est un sous-espace affine de dimension
sont non tous nuls,
est un sous-espace affine de dimension 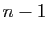 dans
dans
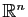 ,
que l'on appelle un hyperplan.
Résoudre un système de
,
que l'on appelle un hyperplan.
Résoudre un système de 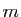 équations, c'est décrire
l'intersection de
équations, c'est décrire
l'intersection de 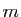 hyperplans dans
hyperplans dans
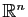 . Cette intersection peut
être vide, mais si elle ne l'est pas, c'est un sous-espace affine de
. Cette intersection peut
être vide, mais si elle ne l'est pas, c'est un sous-espace affine de
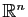 . Nous le démontrerons à la section suivante.
. Nous le démontrerons à la section suivante.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
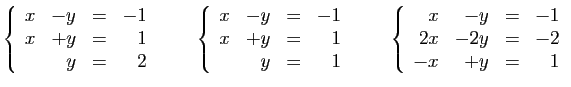
![]() ,
, ![]() ,
, ![]() sont les droites correspondant aux trois
équations du système.
sont les droites correspondant aux trois
équations du système.
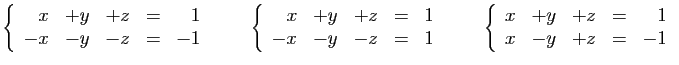
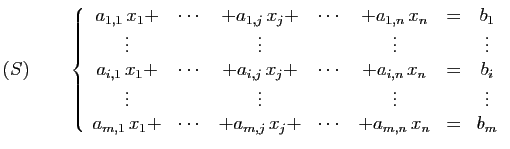
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales