Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
On considère un système 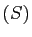 de
de 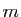 équations à
équations à 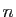 inconnues.
inconnues.
- Qu'appelle-t-on système homogène associé à
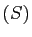 ?
?
- Démontrer que l'ensemble des solutions du système homogène
associé, noté
 , est un sous-espace vectoriel de
, est un sous-espace vectoriel de
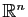 .
.
- En supposant que l'ensemble des solutions de
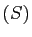 est non vide,
démontrer que c'est un espace affine, dont l'espace vectoriel
associé est l'ensemble des solutions de
est non vide,
démontrer que c'est un espace affine, dont l'espace vectoriel
associé est l'ensemble des solutions de  .
.
- Qu'appelle-t-on forme échelonnée pour le système
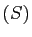 ?
?
- Qu'est ce que le rang du système
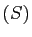 ? Comment
détermine-t-on le rang à partir de la forme échelonnée ?
? Comment
détermine-t-on le rang à partir de la forme échelonnée ?
Exercice 1 :
Soient 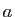 et
et 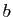 deux paramètres réels.
On considère le système :
deux paramètres réels.
On considère le système :
- Mettre le système
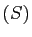 sous forme échelonnée, discuter son
rang selon les valeurs de
sous forme échelonnée, discuter son
rang selon les valeurs de 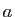 et
et 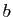 .
.
- Si
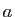 et
et 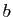 sont tous les deux non nuls, montrer que le système a
une solution unique, et donner l'expression de cette solution en
fonction de
sont tous les deux non nuls, montrer que le système a
une solution unique, et donner l'expression de cette solution en
fonction de 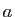 et
et 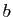 .
.
- Pour
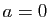 , donner des équations paramétriques de l'ensemble des
solutions de
, donner des équations paramétriques de l'ensemble des
solutions de 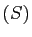 .
.
Exercice 2 :
On considère un espace affine de dimension 3, muni d'un repère
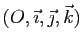 . Soit
. Soit 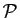 le plan d'équation implicite
le plan d'équation implicite 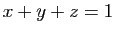 .
Soient
.
Soient 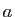 et
et 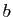 deux paramètres réels.
Soit
deux paramètres réels.
Soit 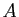 le point de coordonnées
le point de coordonnées 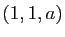 dans le repère
dans le repère
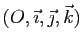 et
et 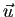 le vecteur de
coordonnées
le vecteur de
coordonnées 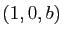 dans la base
dans la base
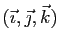 . Soit
. Soit 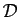 la droite
passant par
la droite
passant par 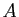 , de vecteur directeur
, de vecteur directeur 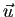 . Le but de l'exercice
est d'étudier l'intersection du plan
. Le but de l'exercice
est d'étudier l'intersection du plan 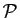 et de la droite
et de la droite
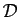 .
.
- Vérifier que le vecteur
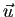 appartient au plan
vectoriel associé à
appartient au plan
vectoriel associé à 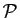 si et seulement si
si et seulement si 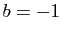 .
.
- Pour
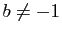 montrer que l'intersection de
montrer que l'intersection de 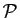 et
et 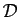 est
réduite à un point.
est
réduite à un point.
- Pour
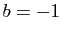 , montrer que l'intersection de
, montrer que l'intersection de 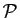 est vide si
est vide si
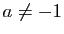 , égale à
, égale à 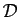 si
si 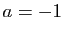 .
.
- Vérifier que
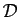 est l'intersection des deux plans
d'équations implicites
est l'intersection des deux plans
d'équations implicites 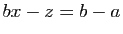 et
et 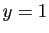 .
Ecrire le système linéaire caractérisant l'intersection de
.
Ecrire le système linéaire caractérisant l'intersection de
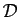 et
et 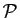 .
.
- Mettre ce système sous forme échelonnée.
- Discuter le rang du système et la dimension de l'ensemble des
solutions selon les valeurs de
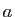 et
et 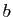 (retrouver les résultats
des questions 1, 2 et 3).
(retrouver les résultats
des questions 1, 2 et 3).
- Pour
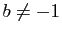 donner
l'expression de la solution du système en fonction de
donner
l'expression de la solution du système en fonction de 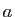 et
et 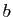 .
.
Exercice 3 :
Soient 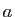 et
et 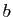 deux paramètres réels.
On considère le système :
deux paramètres réels.
On considère le système :
- Mettre le système
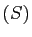 sous forme échelonnée.
sous forme échelonnée.
- Discuter le rang du système selon les valeurs de
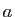 et
et 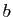 .
.
- Pour
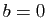 , donner une condition nécessaire et suffisante sur
, donner une condition nécessaire et suffisante sur 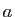 pour que le système
pour que le système 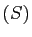 ait des solutions.
ait des solutions.
- Pour
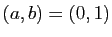 , montrer que l'ensemble des solutions est un plan
affine dont on donnera des équations paramétriques.
, montrer que l'ensemble des solutions est un plan
affine dont on donnera des équations paramétriques.
- Pour
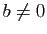 , montrer que le système a une solution unique, dont on
donnera l'expression en fonction de
, montrer que le système a une solution unique, dont on
donnera l'expression en fonction de 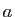 et
et 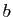 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() de
de ![]() équations à
équations à ![]() inconnues.
inconnues.
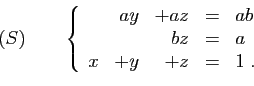
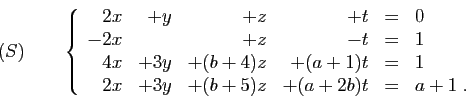
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales