-
- Si un système a 4 équations et 2 inconnues, alors il est impossible.
-
- Si un système a 1 équation et 3 inconnues, alors il a une infinité de solutions.
-
- Si un système a 3 équations, 2 inconnues, et un second membre nul, alors il a au moins une solution.
-
- Si un système a 2 équations, 2 inconnues, et un second membre nul, alors il a exactement une solution.
-
- Si un système a 3 équations et 2 inconnues, et un second membre nul, alors il a une infinité de solutions.
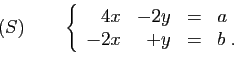
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales