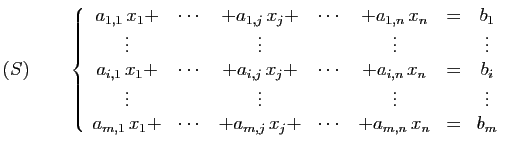
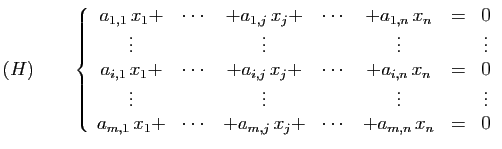
Pour montrer qu'un ensemble non vide est un sous-espace vectoriel de
![]() ,
il suffit de vérifier qu'il est stable par combinaison linéaire,
c'est-à-dire que si deux éléments appartiennent à l'ensemble,
toutes leurs combinaisons linéaires restent dans le même ensemble.
Soient
,
il suffit de vérifier qu'il est stable par combinaison linéaire,
c'est-à-dire que si deux éléments appartiennent à l'ensemble,
toutes leurs combinaisons linéaires restent dans le même ensemble.
Soient
![]() et
et
![]() deux
solutions de
deux
solutions de ![]() ,
, ![]() et
et ![]() deux réels quelconques.
Nous devons vérifier que
deux réels quelconques.
Nous devons vérifier que
![]() est solution de
est solution de ![]() .
Considérons la
.
Considérons la ![]() -ième équation, vérifiée à la fois par
-ième équation, vérifiée à la fois par
![]() et
et ![]() .
.
Réciproquement, on vérifie de la même façon que
tout ![]() -uplet somme de
-uplet somme de ![]() et d'une
solution de
et d'une
solution de ![]() est solution de
est solution de ![]() .
.
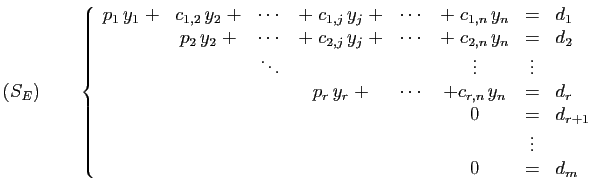
- les inconnues
 de
de 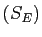 sont celles de
sont celles de 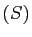 ,
mais dans un ordre qui peut être différent,
,
mais dans un ordre qui peut être différent,
- les coefficients
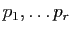 sont tous non nuls.
sont tous non nuls.
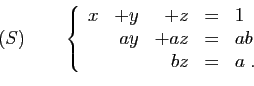
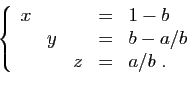
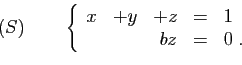
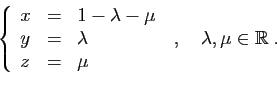
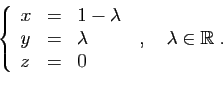
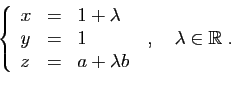
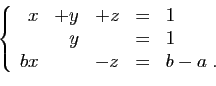
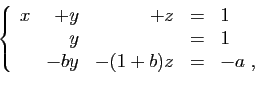
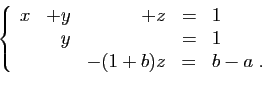
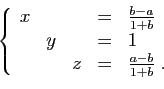
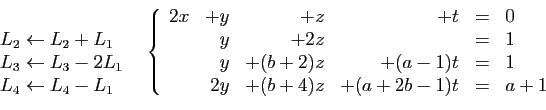
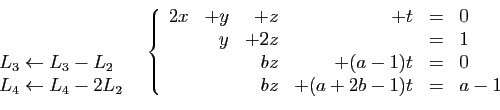
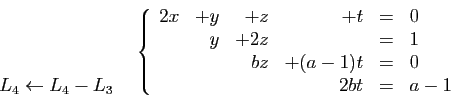
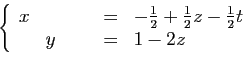
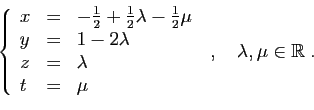
![\begin{displaymath}
\left\{
\begin{array}{lcl}
x&=&-\frac{1}{2}-\frac{(a-1)^2}{4...
...1)^2}{2b^2}\ [1.5ex]
t&=&\frac{a-1}{2b}\;.
\end{array}\right.
\end{displaymath}](img235.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales