Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit
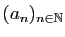 une suite de réels ou de complexes.
une suite de réels ou de complexes.
- Soit
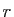 un réel strictement positif. Démontrer que si la suite
un réel strictement positif. Démontrer que si la suite
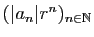 est bornée, alors pour tout
est bornée, alors pour tout 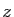 tel que
tel que
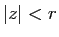 , la série entière
, la série entière
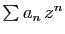 est absolument
convergente.
est absolument
convergente.
- Définir le rayon de convergence de la série entière
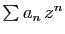 .
.
- On suppose que la suite de terme général
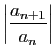 converge vers une limite finie non nulle, notée
converge vers une limite finie non nulle, notée 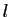 . Montrer que
. Montrer que
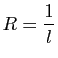 .
.
- On suppose que la suite de terme général
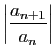 tend vers 0. Montrer que pour tout
tend vers 0. Montrer que pour tout
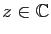 , la série entière
, la série entière
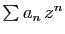 est absolument
convergente.
est absolument
convergente.
- On suppose que la suite de terme général
![$ \displaystyle{\sqrt[n]{\vert a_n\vert}}$](img562.gif) converge vers une limite finie non nulle, notée
converge vers une limite finie non nulle, notée 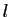 . Montrer que
. Montrer que
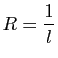 .
.
Exercice 1 :
- Montrer que les séries entières
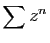 et
et
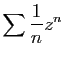 ont pour rayon de convergence
ont pour rayon de convergence
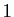 . Pour tout
. Pour tout
![$ x\in ]-1,1[$](img424.gif) , donner la valeur de
, donner la valeur de
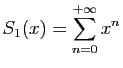
et
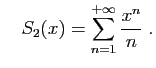
- Démontrer que la série produit
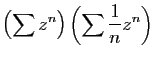 a pour rayon de convergence
a pour rayon de convergence 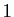 et que pour
tout
et que pour
tout
![$ x\in ]-1,1[$](img424.gif) ,
,
- Pour tout
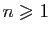 , on pose
, on pose
Montrer que
En déduire que la série de terme
général 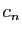 a pour rayon de convergence
a pour rayon de convergence 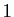 .
.
- Pour tout
![$ x\in ]-1,1[$](img424.gif) , on note
, on note
Quel est le développement en série de 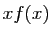 ? En déduire que
? En déduire que
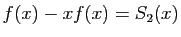 et retrouver le résultat de la question 2.
et retrouver le résultat de la question 2.
- Soit
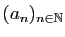 une suite (quelconque)
de réels strictement positifs. Pour
tout
une suite (quelconque)
de réels strictement positifs. Pour
tout
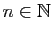 . On pose
. On pose
On note 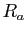 et
et 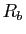 les rayons de convergence respectifs des
séries entières
les rayons de convergence respectifs des
séries entières
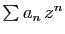 et
et
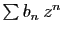 . Montrer que
. Montrer que
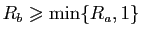 .
.
- On suppose désormais que la suite
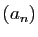 tend vers 0 et que
la série
tend vers 0 et que
la série 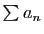 diverge. Montrer que
diverge. Montrer que 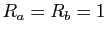 .
.
- Pour tout
![$ x\in ]-1,1[$](img424.gif) , on pose
, on pose
Démontrer que pour tout
![$ x\in ]-1,1[$](img424.gif) ,
,
Exercice 2 :
Le nombre moyen 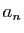 de comparaisons effectuées par l'algorithme
de tri rapide Quicksort, pour une liste de
de comparaisons effectuées par l'algorithme
de tri rapide Quicksort, pour une liste de 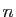 nombres ordonnés au
hasard vérifie
nombres ordonnés au
hasard vérifie 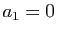 et pour tout
et pour tout 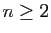 :
:
- Montrer que pour tout
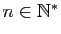
En déduire que la série entière
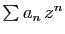 a pour rayon de
convergence
a pour rayon de
convergence 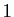 .
.
- Pour tout
![$ x\in ]-1,1[$](img424.gif) , calculer la somme de la série
, calculer la somme de la série
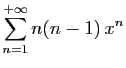 .
.
- Pour tout
![$ x\in ]-1,1[$](img424.gif) , on note
, on note  la somme de la série
la somme de la série
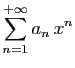 . Montrer que
. Montrer que
(On pourra utiliser l'exercice précédent).
- Montrer que
 est solution de l'équation différentielle
est solution de l'équation différentielle
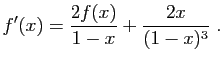 |
(E) |
- On considère l'équation différentielle
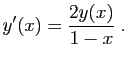 |
(H) |
Soit 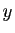 une solution de (H) développable en série entière en 0 :
une solution de (H) développable en série entière en 0 :
Montrer que les 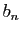 vérifient l'équation de récurrence
vérifient l'équation de récurrence
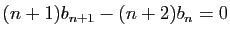 .
.
- En déduire que pour tout
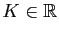 , la fonction
, la fonction 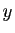 définie par
définie par
est solution de (H) sur ![$ ]-1,1[$](img476.gif) .
.
- Vérifier que l'unique solution de l'équation différentielle (E),
vérifiant
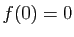 est :
est :
- En déduire que pour tout
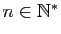 :
:
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() une suite de réels ou de complexes.
une suite de réels ou de complexes.
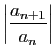 converge vers une limite finie non nulle, notée
converge vers une limite finie non nulle, notée 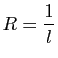 .
.
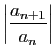 tend vers 0. Montrer que pour tout
tend vers 0. Montrer que pour tout
![$ \displaystyle{\sqrt[n]{\vert a_n\vert}}$](img562.gif) converge vers une limite finie non nulle, notée
converge vers une limite finie non nulle, notée 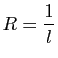 .
.
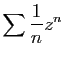 ont pour rayon de convergence
ont pour rayon de convergence
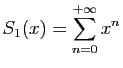 et
et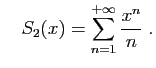
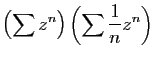 a pour rayon de convergence
a pour rayon de convergence 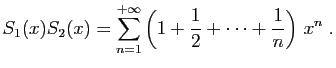
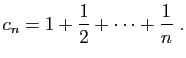
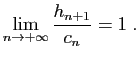
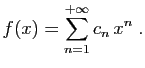
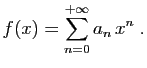
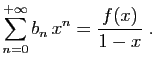
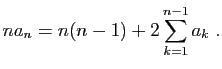
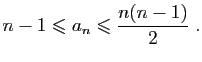
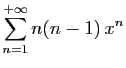 .
.
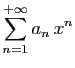 . Montrer que
. Montrer que
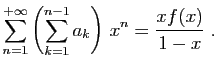
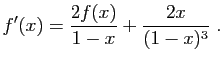
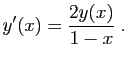
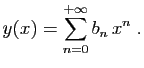
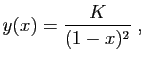
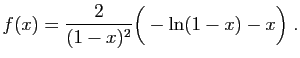
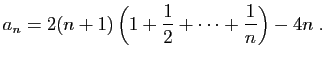
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales