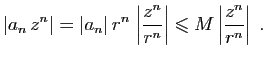
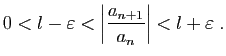
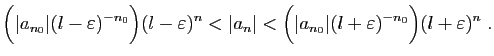
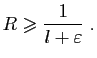
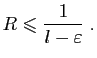
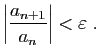
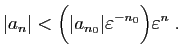
![$\displaystyle l-\varepsilon <\sqrt[n]{\vert a_n\vert}<l+\varepsilon \;,
$](img613.gif)
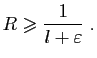
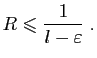
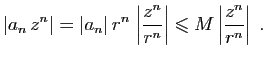
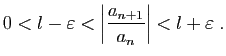
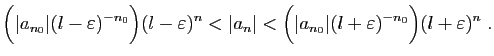
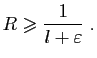
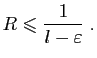
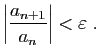
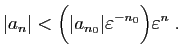
![$\displaystyle l-\varepsilon <\sqrt[n]{\vert a_n\vert}<l+\varepsilon \;,
$](img613.gif)
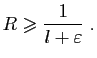
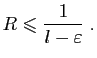
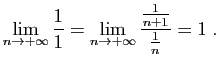
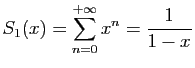 et
et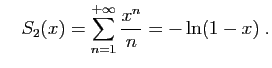
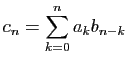
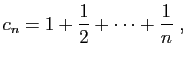
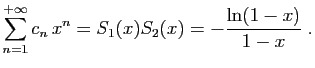
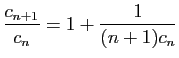
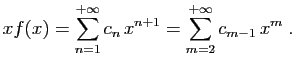
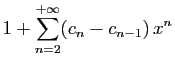 |
|||
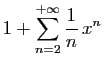 |
|||
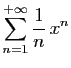 |
|||
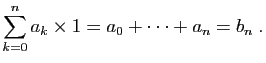
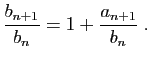
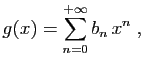
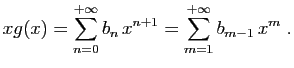
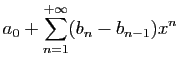 |
|||
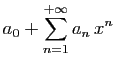 |
|||
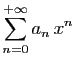 |
|||
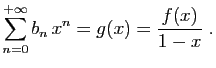
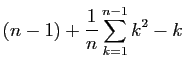 |
|||
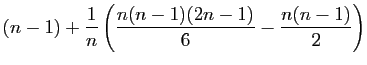 |
|||
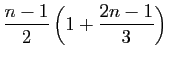 |
|||
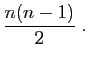 |
En prenant la limite du rapport de deux termes successifs, on
vérifie que les deux séries
![]() et
et
![]() ont pour rayon de convergence
ont pour rayon de convergence ![]() . Par le
théorème de comparaison des séries, la série
. Par le
théorème de comparaison des séries, la série
![]() a
aussi pour rayon de convergence
a
aussi pour rayon de convergence ![]() .
.
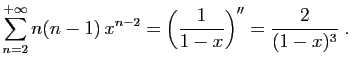
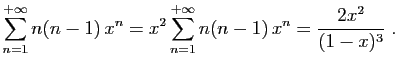
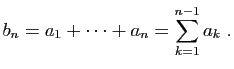
Pour tout
![]() , posons
, posons
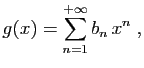
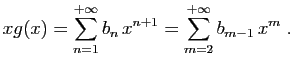
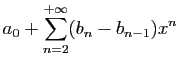 |
|||
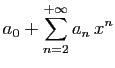 |
|||
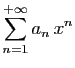 |
|||
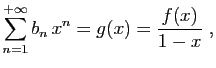
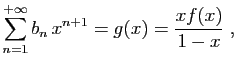
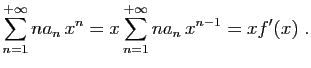
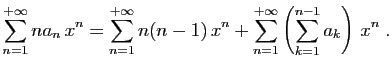
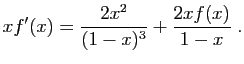
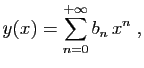
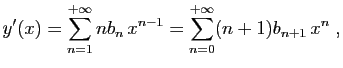
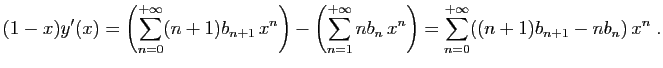
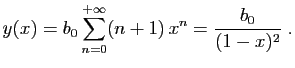
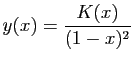 et
et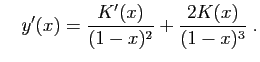
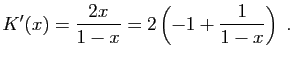
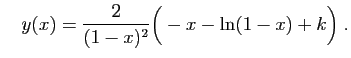
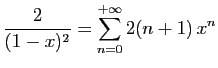 et
et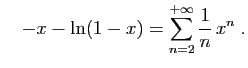
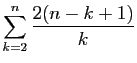 |
|||
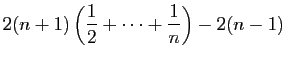 |
|||
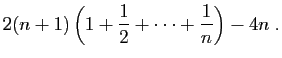 |
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales