-
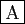
- Si
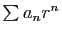 converge, alors
converge, alors
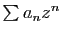 converge,
pour tout
converge,
pour tout 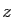 tel que
tel que 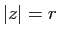 .
.
-
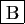
- Si
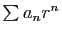 converge, alors
converge, alors
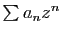 converge,
pour tout
converge,
pour tout 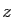 tel que
tel que 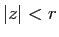 .
.
-
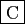
- Si
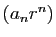 est bornée, alors
est bornée, alors
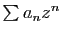 diverge,
pour tout
diverge,
pour tout 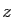 tel que
tel que
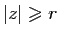 .
.
-
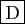
- Si
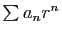 converge absolument, alors
converge absolument, alors
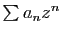 converge,
pour tout
converge,
pour tout 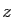 tel que
tel que
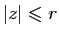 .
.
-
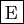
- Si
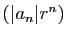 est bornée, alors
est bornée, alors
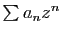 converge,
pour tout
converge,
pour tout 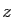 tel que
tel que 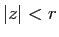 .
.
![$ \displaystyle{\forall z\in ]-1,2[\;,\quad \frac{1}{z+1}+\frac{1}{z-2}
= \sum_{n=0}^{+\infty} ((-1)^n +2^{n+1}) z^n}$](img542.gif)
![$ \displaystyle{\forall z\in ]-2,2[\;,\quad \frac{1}{z-2}
= \sum_{n=0}^{+\infty} (\frac{1}{2^{n}} z^n}$](img543.gif)
![$ \displaystyle{\forall z\in ]-2,2[\;,\quad \frac{1}{z+2}
= \sum_{n=0}^{+\infty} \frac{1}{(-2)^{n+1}} z^n}$](img544.gif)
![$ \displaystyle{\forall z\in ]-\frac{1}{2},\frac{1}{2}[\;,\quad \frac{1}{2z-1}
= \sum_{n=0}^{+\infty} -2^{n+1} z^n}$](img545.gif)
![$ \displaystyle{\forall z\in ]-\frac{1}{2},\frac{1}{2}[\;,\quad \frac{1}{2z+1}
= \sum_{n=0}^{+\infty} -(-2)^{n+1} z^n}$](img546.gif)
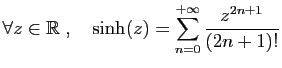
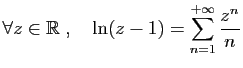
![$ \displaystyle{\forall z\in ]-1,1[\;,\quad \arctan(z)
= \sum_{n=0}^{+\infty} \frac{(-1)^nz^{2n+1}}{2n+1}}$](img549.gif)
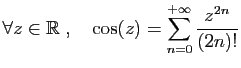
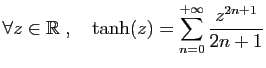
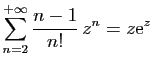
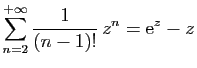
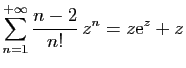
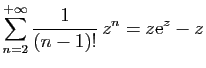
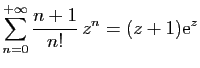
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales