Section : Cours
Avant : Groupes
Après : Sous-groupes

Exemples fondamentaux de groupes finis

Cette partie est consacrée à deux exemples fondamentaux de classes de groupes finis. La première classe est composée de groupes abéliens, la seconde de groupes non abéliens sauf dans des cas dégénérés.

Définition 15   Pour tout entier $ n\geqslant 1$, appelons $ Z_{n}$ le groupe

$\displaystyle Z_{n}=\{0,1,\ldots,n-1\}, $

muni de la loi de composition, notée $ \oplus$, définie comme suit. Si les éléments $ i$ et $ j$ de $ Z_{n}$ sont tels que $ i+j\leqslant n-1$, on pose $ i\oplus j=i+j$. Sinon, $ i+j\geqslant n$ et on pose $ i\oplus j=i+j-n$.

Proposition 6   Pour tout $ n\geqslant 1$, $ (Z_{n},\oplus)$ est un groupe abélien de neutre 0.

Démonstration : Le seul point notable est que l'inverse de 0 vaut 0 et celui d'un élément $ i\neq0$ vaut $ n-i$.$ \square$

On verra plus tard une présentation plus intrinsèque des groupes $ Z_{n}$ comme quotients du groupe $ \mathbb{Z}$ muni de l'addition. Profitons tout de même du moment pour introduire une définition.

Définition 16   Soit $ G$ un groupe de loi de composition $ \ast$ et de neutre $ e$ et soit $ a$ un élément de $ G$. L'ordre de $ a$ est le plus petit entier $ k\geqslant 1$, s'il existe, tel que $ a^{\ast k}=e$. Sinon on dit que l'ordre de $ a$ est infini.

Bien sûr, l'ordre du neutre vaut toujours $ 1$ et l'ordre de tout élément d'un groupe fini de cardinal fini $ n$ est fini et inférieur ou égal à $ n$. Nous verrons bientôt que c'est forcément un diviseur de $ n$.

Outre les groupes $ Z_{n}$, les groupes les plus directement utilisables sont sans doute ceux qui interviennent en géométrie. Ce sont des groupes de transformations «respectant»  telle ou telle propriété ; ainsi les isométries, qui conservent les distances, ou les similitudes, qui conservent les angles. Et ils constituent notre deuxième classe d'exemples.

Tous ces groupes ont le point commun d'avoir pour loi de composition $ \circ$, la composition des applications, et d'être formés de bijections.

Fondamentale (quoique très facile) sera donc l'affirmation suivante.

Proposition 7   Soit $ E$ un ensemble. L'ensemble des bijections de $ E$ dans lui-même forme un groupe pour la composition.

Démonstration : Tout est très simple. On vérifie que, pour toute bijection $ f$ de $ E$, la bijection réciproque est un symétrique de $ f$ ; que la composée de deux bijections est une bijection, par exemple parce que $ g^{-1}\circ f^{-1}$ se révèle un inverse de $ f\circ g$ ; que la composition est associative ; et enfin que $ \mathrm{id}_E$ est son neutre. On a déjà fini !$ \square$

Notation 5   Soit $ E$ un ensemble. L'ensemble des bijections de $ E$ dans lui-même est noté $ {\cal S}(E)$.

On utilise souvent (au moins en mathématiques, en informatique et en analyse du génome) le cas particulier du groupe des bijections d'un ensemble fini. L'archétype d'un tel ensemble fini étant $ \{1,\ldots,n\}$, cela justifie d'introduire une toute spéciale notation.


Notation 6   Pour tout entier $ n\geqslant 1$, on note $ \mathbb{N}_{n}=\{1,2,\ldots,n\}$. L'ensemble des bijections de $ \mathbb{N}_{n}$ s'appelle le groupe des permutations sur $ n$ éléments. On le note $ {\cal S}_n$.

Tentons de découvrir comment fonctionne le groupe des permutations $ {\cal S}_n$ pour $ n$ pas trop gros ; il vaut même mieux prendre $ n$ franchement petit, car $ {\cal S}_n$ possédant $ n!$ éléments, on serait vite débordé.

Pour $ n=1$, le groupe n'a qu'un élément ; sa table est vite tracée.


\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert} \hline \circ&e\\ \hline\hline e&e\\ \hline \end{array}\end{displaymath}

Pour $ n=2$, il y a deux bijections de $ \{1,2\}$ : celle qui échange les deux éléments, qu'on notera $ \tau$, et l'identité.

La table du groupe est donc la suivante.


\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert} \hline \circ&... ...u\\ \hline\hline e&e&\tau\\ \tau&\tau&e\\ \hline \end{array}\end{displaymath}

À partir de $ n=3$, les calculs complets seraient nettement plus fastidieux. On va en profiter pour introduire des notations et énumérer les ensembles $ {\cal S}_{n}$.

Notation 7   On dispose de plusieurs notations pour désigner une permutation $ s$ élément de $ {\cal S}_{n}$. La première est

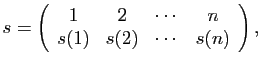
$\displaystyle s=\left(\begin{array}{cccc}1 & 2 & \cdots & n\\ s(1) & s(2) & \cdots & s(n)\end{array}\right), $

que l'on abrège parfois en

$\displaystyle s=(s(1),s(2),\ldots, s(n)). $

Définition 17   Une orbite d'une permutation $ s$ élément de $ {\cal S}_{n}$ est une partie

$\displaystyle \{s^{\circ k}(i) ; k\geqslant 1\},\quad i\in\mathbb{N}_{n}. $

On peut expliciter la structure des orbites comme suit.

Proposition 8   Pour toute permutation $ s$ et tout élément $ i$ de $ \mathbb{N}_{n}$, il existe un entier $ k\geqslant 1$ tel que $ s^{\circ k}(i)=i$. Le plus petit entier $ k\geqslant 1$ qui vérifie cette propriété est le cardinal de l'orbite de $ i$ et s'appelle la taille de l'orbite de $ i$.

Définition 18   Un cycle $ s$ est un élément de $ {\cal S}_{n}$ qui possède exactement une orbite de longueur différente de $ 1$.

Pour tout cycle $ s$ de longueur $ k\geqslant 2$, il existe donc une partie $ S\subset\mathbb{N}_{n}$ de cardinal $ k$ telle que $ s(i)=i$ pour tout élément $ i$ de $ \mathbb{N}_{n}\setminus S$. De plus, on peut numéroter les éléments de $ S$ comme suit :

$\displaystyle S=\{i_{1},i_{2},\ldots, i_{k}\},\quad s(i_{j})=i_{j+1}, 1\leqslant j\leqslant k-1, s(i_{k})=i_{1}. $

Notation 8   On désigne le cycle $ s$ de longueur $ k\geqslant 2$ ci-dessus par l'écriture

$\displaystyle s=(i_1i_{2}\ldots i_{k}). $


Avertissement On aura remarqué que la notation 8 est affreusement proche de l'écriture abrégée d'une permutation quelconque donnée dans la notation 7, la seule différence portant sur la présence ou l'absence de virgules.

Bien sûr, si le nombre d'entiers figurant dans l'écriture de $ s$ est différent de $ n$, on désigne forcément le cycle. Dans le cas contraire, on veillera à ne pas confondre

$\displaystyle a=(123)$   et$\displaystyle \quad e=(1,2,3), $

puisque $ a$ est un cycle de longueur $ 3$ et $ e$ est la permutation identité.

Enfin, remarquons qu'un cycle dispose de plusieurs écritures différentes, par exemple

$\displaystyle a=(123)=(231)=(312). $

Fin de l'avertissement.


Il est à présent facile d'énumérer les éléments de $ {\cal S}_3$ : outre l'identité, que l'on va noter $ e$, il y en a trois d'apparence identique : l'un, que je noterai $ t$, échange $ 1$ et $ 2$ en laissant $ 3$ fixe ; un autre, que je me garderai astucieusement de noter, échange $ 2$ et $ 3$ en laissant $ 1$ fixe ; le dernier échange $ 3$ et $ 1$ en laissant $ 2$ fixe. Enfin deux autres jouent aussi des rôles voisins : l'un, que je noterai $ a$, fait «tourner» les trois éléments de $ \{1,2,3\}$ en envoyant $ 1$ sur $ 2$, $ 2$ sur $ 3$, et $ 3$ sur $ 1$ ; l'autre, dont je remarquerai que c'est le carré de $ a$, les fait «tourner» dans l'autre sens. Ainsi,

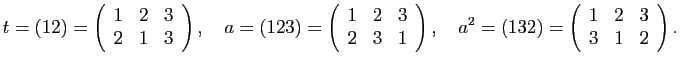
$\displaystyle t=(12)=\left(\begin{array}{ccc}1 & 2 & 3\\ 2 & 1 & 3\end{array}\... ... a^{2}=(132)=\left(\begin{array}{ccc}1 & 2 & 3\\ 3 & 1 & 2\end{array}\right). $

On va remplir la table du groupe par ajouts successifs d'information. L'information la plus récente sera systématiquement portée en gras.

Au point où nous en sommes, il est facile de commencer en remarquant que $ a^3=e$ tandis que $ a^2$, comme on l'a déjà dit, est distinct de $ a$. En outre les trois autres éléments ont un carré égal à $ e$.


\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert ... ...symbol{e}&\\ \hline &&&&&&\boldsymbol{e}\\ \hline \end{array}\end{displaymath}

C'est le bon moment pour glisser une remarque importante : dans la table de composition d'un groupe on trouve chaque élément du groupe une fois et une seule dans chaque ligne, et dans chaque colonne. Sauriez-vous le démontrer ? Sinon, cher lecteur, nous vous conseillons d'arrêter votre lecture et de chercher une démonstration.


Le produit $ at$ ne peut être présent deux fois dans la colonne $ a$, ni deux fois dans la ligne $ t$. Il est donc distinct des éléments qui y figurent déjà, c'est-à-dire de $ e$, de $ a$, de $ a^2$ et de $ t$. C'est donc un cinquième élément, qu'on peut alors faire figurer dans la cinquième ligne et la cinquième colonne du tableau. On calcule au passage sans mal $ (a^2)(at)=(a^3)t=et=t$, et $ (at)t=a(t^2)=ae=a$.


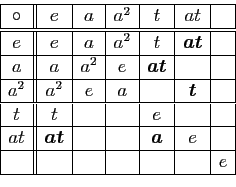
\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert ... ...at}&&&\boldsymbol{a}&e&\\ \hline &&&&&&e\\ \hline \end{array}\end{displaymath}

Puis à son tour, $ a^2t$ ne peut déjà figurer dans la ligne $ a^2$ ni dans la colonne $ t$ : c'est donc le sixième élément. On peut l'ajouter au tableau en complétant par quelques calculs évidents.


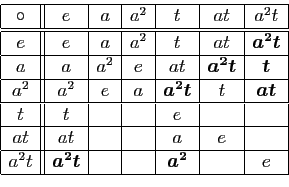
\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert ... ...t&\boldsymbol{a^2t}&&&\boldsymbol{a^2}&&e\\ \hline \end{array}\end{displaymath}

En utilisant toujours l'astuce selon laquelle il ne peut y avoir deux fois la même valeur dans une ligne ni dans une colonne, on arrive à calculer $ (at)(a^2t)$ et $ (a^2t)(at)$ par simple élimination de cinq valeurs impossibles.


\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert ... ... \hline a^2t&a^2t&&&a^2&\boldsymbol{a}&e\\ \hline \end{array}\end{displaymath}

Surprise ! On vient de montrer avec une étonnante économie de calculs que le groupe n'est pas commutatif ; en effet $ (at)(a^2t)\not=(a^2t)(at)$.

Le même truc des répétitions interdites permet de compléter le coin inférieur droit du tableau.


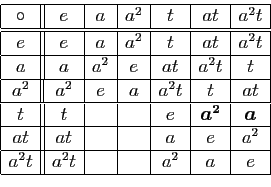
\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert ... ...t&&&a&e&a^2\\ \hline a^2t&a^2t&&&a^2&a&e\\ \hline \end{array}\end{displaymath}

Dernier obstacle inattendu, alors que nous avions presque fini, avec la méthode, maintenant classique pour nous, de remplir les cases par élimination, cette méthode est insuffisante pour remplir les six misérables cases laissées blanches ! Il faut une nouvelle astuce pour passer cet obstacle. Concentrons-nous sur la case correspondant au produit $ ta$. Pour calculer ce produit, bidouillons un peu : $ ta=tae=ta(t^2)=[t(at)]t=a^2t$. Une nouvelle case est remplie :


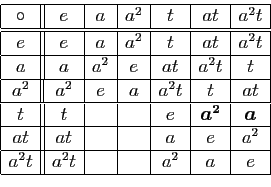
\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert ... ...t&&&a&e&a^2\\ \hline a^2t&a^2t&&&a^2&a&e\\ \hline \end{array}\end{displaymath}

Cette étape franchie, il est désormais très facile de finir de remplir la table en utilisant l'idée simple : pas plus d'une apparition par ligne ou par colonne.


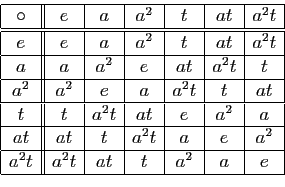
\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert ... ...&a&e&a^2\\ \hline a^2t&a^2t&at&t&a^2&a&e\\ \hline \end{array}\end{displaymath}

On a donc obtenu la table complète de la loi de composition $ \circ$ sur $ {\cal S}_{3}$, en n'utilisant que des techniques élémentaires.


Section : Cours
Avant : Groupes
Après : Sous-groupes


         © UJF Grenoble, 2011                              Mentions légales