Section : Cours
Avant : Relations
Après : Groupes

Lois de composition et morphismes

Définition 8   On appelle loi de composition sur un ensemble $ E$ une application de $ E\times E$ vers $ E$.

En fait, bien que cette définition soit générale, on n'aurait pas l'idée d'appeler «loi de composition» n'importe quelle application de $ E\times E$ vers $ E$ ; le vocable n'est utilisé que quand il est naturel de noter l'application par un symbole opératoire. Des exemples typiques de lois de composition sont l'addition $ +$ de $ \mathbb{R}^2$ vers $ \mathbb{R}$, qui associe $ x+y$ à $ (x,y)$ ; ou bien la loi de composition $ \circ$ sur l'ensemble $ E^E$ des applications de $ E$ vers $ E$, qui associe l'application $ f\circ g$ au couple d'applications $ (f,g)$. Pour des lois de composition abstraites, le symbole opératoire $ \ast$ a été à la mode et nous l'utiliserons occasionnellement, surtout au début, mais nous nous contenterons rapidement de la notation multiplicative $ a\cdot b$, ou même simplement $ ab$, pour l'élément obtenu en appliquant la loi de composition à $ (a,b)$.

Voici un peu de vocabulaire au sujet des lois de composition.

Définition 9   Soit $ \ast$ une loi de composition sur un ensemble $ E$.
  1. On dit que $ \ast$ est commutative lorsque pour tous éléments $ a$ et $ b$ de $ E$,

    $\displaystyle a\ast b=b\ast a.$

  2. On dit que $ \ast$ est associative lorsque pour tous éléments $ a$, $ b$ et $ c$ de $ E$,

    $\displaystyle (a\ast b)\ast c=a\ast (b\ast c).$

  3. On dit qu'un élément $ e$ de $ E$ est élément neutre pour $ \ast$ lorsque pour tout élément $ a$ de $ E$,

    $\displaystyle a\ast e=e\ast a=a.$

La cohérence de ce qui suit nécessite d'énoncer tout de suite un résultat simplissime.

Proposition 2   Une loi de composition possède au plus un élément neutre.

Démonstration : Soit $ e_1$ et $ e_2$ deux éléments neutres pour une loi de composition $ \ast$. Comme $ e_2$ est neutre, $ e_1\ast e_2=e_1$ et comme $ e_1$ est neutre, $ e_1\ast e_2=e_2$. Donc $ e_1=e_2$.$ \square$

On parlera donc de l'élément neutre avec l'article défini, lorsqu'il existe un élément neutre.

Définition 10   Soit $ \ast$ une loi de composition sur un ensemble $ E$ admettant un élément neutre noté $ e$ et soit $ a$ un élément de $ E$. On dit qu'un élément $ b$ de $ E$ est symétrique (ou inverse) de $ a$ lorsque

$\displaystyle a\ast b=b\ast a=e.$

Là encore, glissons sans tarder une évidence.

Proposition 3   Soit $ \ast$ une loi de composition sur un ensemble $ E$, associative et possédant un élément neutre. Chaque élément possède au plus un symétrique.

Démonstration : Soit $ e$ le neutre de $ \ast$, soit $ a$ un élément de $ E$ et soient $ b_1$ et $ b_2$ deux symétriques de $ a$. Alors d'une part $ (b_1\ast a)\ast b_2=e\ast b_2=b_2$ et d'autre part $ b_1\ast (a\ast b_2)=b_1\ast e=b_1$. Par associativité de la loi de composition, $ (b_1\ast a)\ast b_2=b_1\ast (a\ast b_2)$, d'où $ b_1=b_2$.$ \square$

Les lois de composition intéressantes étant en pratique associatives, on pourra donc faire plein usage de la notation suivante.

Notation 3   Le symétrique d'un élément $ a$ est noté $ a^{-1}$.

Maintenant que nous savons manipuler une loi de composition sur un seul ensemble, apprenons à évoluer d'un ensemble muni d'une loi de composition vers un autre.

Définition 11   Soit $ E$ un ensemble muni d'une loi de composition $ \ast$ et $ F$ un ensemble muni d'une loi de composition $ \cdot$. On dit qu'une application $ f \colon E\to F$ est un morphisme lorsque pour tous éléments $ a$ et $ b$ de $ E$, on a l'identité :

$\displaystyle f(a\ast b)=f(a)\cdot f(b). $

Définition 12   Un morphisme bijectif est appelé un isomorphisme.

Il semble plus facile d'expliquer la notion d'isomorphisme que celle de morphisme en général ; deux lois de composition sur deux ensembles fourniront des structures isomorphes lorsque ces deux lois de composition agissent de la même façon, seuls les noms des éléments changeant. La phrase précédente n'étant peut-être pas si claire que cela, donnons plutôt des exemples, c'est toujours bien les exemples.

Exemple 5   Considérons tout d'abord la bijection $ \sigma$ de l'ensemble $ E=\{0,1,2,3\}$ définie par

$\displaystyle \sigma(0)=1,\quad\sigma(1)=2,\quad\sigma(2)=3,\quad\sigma(3)=0. $

Avec à peine un peu de bon sens (tout mathématicien pense très vite à $ \sigma$ comme «faisant tourner» les quatre éléments de $ E$), on voit sans guère de calculs que $ \sigma\circ\sigma$ est la bijection $ \tau$ de $ E$ définie par

$\displaystyle \tau(0)=2,\quad\tau(1)=3,\quad\tau(2)=0,\quad\tau(3)=1, $

puis que $ \sigma\circ\sigma\circ\sigma$ est la bijection $ \varrho$ de $ E$ définie par

$\displaystyle \varrho(0)=3,\quad\varrho(1)=0,\quad\varrho(2)=1,\quad\varrho(3)=2, $

et enfin que $ \sigma\circ\sigma\circ\sigma\circ\sigma$ est tout simplement l'identité de $ E$, que l'on note désormais $ e$.

Pour abréger les calculs qui suivent, introduisons une notation.

Notation 4   Pour tout élément $ a$ d'un ensemble $ E$ muni d'une loi de composition $ \ast$ et pour tout entier $ n\geqslant 1$, notons $ a^{\ast n}$ la composition de $ a$ avec lui-même $ n$ fois. Ainsi, $ a^{\ast 1}=a$ puis, pour tout $ n\geqslant 1$, $ a^{\ast n+1}=a^{\ast n}\ast a$. Si la loi de composition $ \ast$ est munie d'un neutre $ e$, on notera aussi $ a^{\ast 0}=e$. Enfin, on abrège souvent $ a^{\ast n}$ en $ a^{n}$.

En utilisant cette notation, on peut très facilement calculer tous les produits deux à deux des bijections introduites ici ; par exemple $ \varrho\circ\tau=\sigma^3\circ\sigma^2= \sigma^5=\sigma^4\circ\sigma=e \circ\sigma=\sigma$.

On considère alors l'ensemble $ S=\{ e,\sigma,\tau,\varrho\}$ et on voit que $ \circ$ est une loi de composition sur ce sous-ensemble de $ E^E$, qui sera agréablement décrite par le tableau suivant, que l'on appelle une table de composition.


\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert}... ...a\\ \hline \varrho&\varrho&e&\sigma&\tau\\ \hline \end{array}\end{displaymath}

Considérons à présent l'ensemble des nombres complexes dont la puissance quatrième vaut $ 1$, c'est-à-dire l'ensemble $ F =\{1,\mathrm{i},{-1},-\mathrm{i}\}$. Il est très facile de constater que la multiplication des nombres complexes définit une loi de composition sur $ F$, dont la table est donnée ci-dessous.


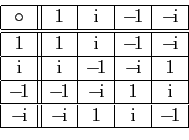
\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert}... ...mathrm{i}&-\!\mathrm{i}&1&\mathrm{i}&-\!1\\ \hline \end{array}\end{displaymath}

Visuellement, on retrouve la même table, seuls les noms des éléments ont changé. C'est signe qu'il y a un isomorphisme camouflé. On le détectera facilement ; c'est bien sûr l'application $ g$ de $ E$ vers $ F$ définie par :

$\displaystyle g(e )=1\qquad g(\sigma)=\mathrm{i}\qquad g(\tau)={-1}\qquad g(\varrho)=-\mathrm{i}. $

Exemple 6   Soit $ R$ l'ensemble des rotations de centre $ (0,0)$ dans le plan, et soit $ \mathbb{U}$ le cercle-unité de $ \mathbb{C}$, c'est-à-dire l'ensemble des nombres complexes de module 1. Les lois de composition respectivement envisagées sur $ R$ et sur $ \mathbb{U}$ sont la composition des applications et la multiplication. On définit une application $ f \colon R\to{\mathbb{U}}$ en envoyant la rotation d'angle $ \theta$ sur le nombre $ \mathrm{e}^{\mathrm{i}\theta}$.

Il faut tout d'abord se soucier de vérifier que cette définition n'est pas ambiguë, car elle n'est pas loin de l'être ! Une rotation peut en effet être caractérisée par plusieurs angles (tourner d'un quart de tour dans le sens trigonométrique, c'est aussi tourner de trois quarts de tour dans le sens des aiguilles d'une montre), mais deux angles distincts $ \theta_1$ et $ \theta_2$ correspondant à la même bijection diffèrent d'un multiple entier de $ 2\pi$ ; il existe donc un entier $ k\in\mathbb{Z}$ tel que $ \theta_2=\theta_1+2k\pi$. Les valeurs $ \mathrm{e}^{\mathrm{i}\theta_1}$ et

$\displaystyle \mathrm{e}^{\mathrm{i}\theta_2}=\mathrm{e}^{\mathrm{i}\theta_1+2k... ...hrm{i}\theta_1}(\mathrm{e}^{2\mathrm{i}\pi})^k=\mathrm{e}^{\mathrm{i}\theta_1} $

sont donc égales, et l'application $ f$ est bien définie.

Une fois cette mise au point effectuée, vérifier que $ f$ est un morphisme est sans problème : si $ \varrho_1$ est la rotation d'angle $ \theta_1$ et $ \varrho_2$ la rotation d'angle $ \theta_2$, la composée $ \varrho_1\circ \varrho_2$ est la rotation $ \varrho$ d'angle $ \theta_1+\theta_2$, et on a donc :

$\displaystyle f(\varrho_1\circ\varrho_2)=f(\varrho)=\mathrm{e}^{\mathrm{i}(\the... ...^{\mathrm{i}\theta_1}\mathrm{e}^{\mathrm{i}\theta_2}=f(\varrho_1)f(\varrho_2). $

Montrer que $ f$ est bijective n'est pas difficile ; on en conclut que $ f$ est un isomorphisme, en d'autres termes que l'étude des nombres complexes de module 1 nous instruira sur le fonctionnement des rotations.

Exemple 7   Voici enfin un morphisme qui n'est pas un isomorphisme et qui est pourtant une simple variante du précédent. Considérons l'application $ F$ de $ \mathbb{R}$ (muni de l'addition) vers $ \mathbb{U}$ (le même qu'à l'exemple précédent, muni de la multiplication) définie par $ F(\theta)=\mathrm{e}^{\mathrm{i}\theta}$. On voit facilement que $ F$ est un morphisme, mais comme, par exemple, $ F(0)=F(2\pi)$, $ F$ n'est pas une bijection donc pas un isomorphisme.

À l'évidence (et c'est sans doute ce que vous fîtes au lycée), on peut voir $ F$ comme l'application qui «enroule» de façon régulière une corde (la droite $ \mathbb{R}$) sur une roue (le cercle $ \mathbb{U}$), encore et encore.


Section : Cours
Avant : Relations
Après : Groupes


         © UJF Grenoble, 2011                              Mentions légales