Corps des fractions rationnelles

Le concept est très simple : les fractions rationnelles sont les expressions de la forme $\displaystyle\frac{P}{Q}$ où

sont des polynômes. Une mise en forme totalement rigoureuse demande un effort un peu disproportionné par rapport au caractère intuitif de l'objet à construire.

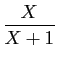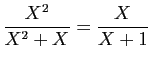La première idée qui peut venir à l'esprit est de tenter de modéliser la fraction $\displaystyle\frac{P}{Q}$ par le couple qui contient à première vue la même information : ainsi la fraction $\displaystyle\frac{X}{X+1}$ correspondra au couple . Une telle idée nous met sur la bonne piste, mais elle se heurte à un problème : le couple représentera la fraction $\displaystyle\frac{X^2}{X^2+X}=\displaystyle\frac{X}{X+1}$ ; la même fraction correspond donc à plusieurs couples, et l'ensemble de tous les couples est donc trop gros.

On pourrait penser à n'utiliser que des couples avec et premiers entre eux ; c'est vraisemblablement faisable, mais la preuve risque d'être extrêmement lourde, avec des pgcd à simplifier de partout.

Non, décidément, on ne fera rien de simple si on n'a pas compris ce qu'est un ensemble-quotient, alors que si on maîtrise cette notion, la preuve est longue à écrire, mais sans obstacles.

Dans tout le chapitre, $\mathbb{K}$ désigne un corps commutatif. Notons $A=\mathbb{K}[X]$ . La construction utilise simplement le fait que est un anneau intègre, et nullement en réalité que est l'anneau des polynômes.

Définition 18 Soit un anneau intègre, 0 son neutre pour l'addition, et l'ensemble

$\displaystyle C=A\times (A\setminus\{0\}).$

Sur on introduit deux opérations et $\times$ définies comme suit : pour tous et de , on pose

$\displaystyle (P_1,Q_1) \times(P_2,Q_2)=(P_1P_2,Q_1Q_2)\qquad (P_1,Q_1)+ (P_2,Q_2)=(P_1Q_2+P_2Q_1,Q_1Q_2).$

On notera qu'on utilise très discrètement l'intégrité de

pour justifier que le produit

qui intervient dans les formules n'est pas nul, donc que la somme et le produit d'éléments de

appartiennent effectivement à

Signalons une fois encore que les deux formules de la définition précédente se comprennent aisément si on a en tête qu'un couple a vocation à décrire la fraction $\displaystyle\frac{P}{Q}$ (qui n'aura un sens propre qu'une fois la construction terminée) : elles sont les reproductions des formules qu'on sait bien utiliser pour multiplier ou additionner des fractions.

L'ensemble a une bonne tête vu de loin, mais de près il est trop gros. Pour le faire maigrir, introduisons une relation d'équivalence $\mathcal{R}$ sur .

Définition 19 Pour tous et de ,

$\displaystyle (P_1,Q_1)\mathcal{R}(P_2,Q_2)\qquad{\rm lorsque}\qquad P_1Q_2=P_2Q_1.$

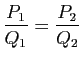Si nous savions déjà donner un sens aux barres de fractions, nous aurions écrit la condition sous la forme $\displaystyle\frac{P_1}{Q_1}=\frac{P_2}{Q_2}$ , la rendant ainsi compréhensible, mais comme ce symbole ne nous sera disponible qu'une fois finie la construction, on a dû donner une forme moins limpide.

Proposition 16 La relation $\mathcal{R}$ est une relation d'équivalence sur .

Démonstration : En effet, et impliquent , voyez-vous. (Indication : comme $Q_{2}\neq0$ , on calcule $P_{1}Q_{3}Q_{2}$ .) $\square$

Notation 8 On note l'ensemble-quotient $C/\mathcal{R}$ et $\mathfrak{cl}(P,Q)$ la classe d'un élément de .

On va alors définir des opérations et $\times$ sur ; le principe est le même que celui qui nous a permis de définir addition et multiplication sur $\mathbb{Z}/n\mathbb{Z}$ : on définit simplement ces opérations sur des représentants des classes d'équivalence, et on vérifie méthodiquement que le résultat obtenu ne dépend pas de la classe utilisée.

Définition 20 Pour $\mathfrak{cl}(P_1,Q_1)$ et $\mathfrak{cl}(P_2,Q_2)$ éléments de , on note

$\displaystyle \mathfrak{cl}(P_1,Q_1) +\mathfrak{cl}(P_2,Q_2)= \mathfrak{cl}\left((P_1,Q_1)+(P_2,Q_2)\right).$

$\displaystyle \mathfrak{cl}(P_1,Q_1) \times\mathfrak{cl}(P_2,Q_2)= \mathfrak{cl}\left((P_1,Q_1) \times(P_2,Q_2)\right),$

Cette «définition» n'en sera une qu'une fois vérifiée la proposition suivante.

Proposition 17 Le résultat des opérations et $\times$ définies sur ne dépend pas des représentants choisis.

Démonstration : On fait la vérification soigneusement pour l'addition, avec «renvoi au lecteur» pour la multiplication.

Soit un représentant quelconque de la classe de et un représentant quelconque de la classe de . Il faut vérifier que

$\displaystyle (P_1,Q_1)+ (P_2,Q_2)=(P_1Q_2+P_2Q_1,Q_1Q_2)$

$\displaystyle (P_3,Q_3)+ (P_4,Q_4)=(P_3Q_4+P_4Q_3,Q_3Q_4),$

sont bien dans la même classe.

Cela revient à comparer les produits $P_{5}$ et $P_{6}$ définis par :

$\displaystyle P_{5}=(P_1Q_2+P_2Q_1)Q_3Q_4,\qquad P_{6}=(P_3Q_4+P_4Q_3)Q_1Q_2.$

On dispose pour ce faire des égalités

, issues respectivement des relations $(P_1,Q_1)\mathcal{R}(P_3,Q_3)$ et $(P_2,Q_2)\mathcal{R}(P_4,Q_4)$ . La vérification est alors directe :

$\displaystyle P_{5}=P_1Q_3Q_2Q_4+P_2Q_4Q_1Q_3= P_3Q_1Q_2Q_4+P_4Q_2Q_1Q_3=P_{6}.$

$\square$

Notation 9 Quand $A=\mathbb{K}[X]$ , on note $\mathbb{K}(X)$ l'ensemble $B=C/\mathcal{R}$ ainsi construit.

On a donc bien construit un ensemble $\mathbb{K}(X)$ puis une addition et une multiplication sur cet ensemble.

Théorème 5 L'ensemble $\mathbb{K}(X)$ muni des lois et $\times$ est un corps commutatif.

Démonstration : La vérification de toutes les propriétés de la définition d'un corps commutatif est simple, méthodique et lourde. On se bornera ici à justifier l'existence de l'inverse.

Si une classe $\mathfrak{cl}(P_1,Q_1)$ n'est pas nulle, on remarque d'abord que $P_1\not=0$ , puisque $\mathfrak{cl}(P_1,Q_1)\not=\mathfrak{cl}(0,1)$ . La classe $\mathfrak{cl}(Q_1,P_1)$ existe donc ; ce sera l'inverse de $\mathfrak{cl}(P_1,Q_1)$ : en effet le produit des deux est $\mathfrak{cl}(Q_1P_1,P_1Q_1)$ qui est égal à la classe de qui est le neutre pour la multiplication. $\square$

Proposition 18 L'anneau $\mathbb{K}[X]$ est inclus dans $\mathbb{K}(X)$ ; plus précisément, il existe un morphisme d'anneaux $j:\mathbb{K}[X]\to\mathbb{K}(X)$ qui est injectif. Tout élément de $\mathbb{K}(X)$ peut s'écrire comme $j(P)j(Q)^{-1}$ pour et dans $\mathbb{K}[X]$ et $Q\neq0$ .

Démonstration : Soit

l'application définie par $j(P)=\mathfrak{cl}(P,1)$ . Il est très facile de vérifier que

transforme addition en addition et multiplication en multiplication ; son injectivité peut seule interpeller. Mais puisque cette transformation est un morphisme de groupes additifs, l'injectivité se laisse montrer à coups de noyaux ; et effectivement si un polynôme

est envoyé sur le neutre additif de $\mathbb{K}(X)$ qui est la classe de

, c'est que $(P,1)\mathcal{R}(0,1)$ et donc que

: le noyau est bien réduit au seul polynôme nul. Enfin,

$\displaystyle \mathfrak{cl}(P,Q)=\mathfrak{cl}(P,1)\mathfrak{cl}(1,Q) =\mathfrak{cl}(P,1)\left[\mathfrak{cl}(Q,1)\right]^{-1} =j(P)j(Q)^{-1}.$

$\square$

Notation 10 On note ou $\displaystyle\frac{P}{Q}$ l'élément $\mathfrak{cl}(P,Q)$ de $\mathbb{K}(X)$ .