Formule de Taylor pour les polynômes

Alors que pour des fonctions d'une variable réelle en général, la formule de Taylor ne peut tomber juste puisqu'elle consiste à approcher la fonction par une fonction polynomiale et que la fonction quelconque n'est précisément en général pas polynomiale, pour des polynômes, la formule analogue ne contient pas de reste.

Une petite subtilité apparaît dans les divisions par des factorielles qui enjolivent la formule. En effet dans un anneau commutatif quelconque, mais même dans un corps commutatif, on ne peut pas toujours diviser par une factorielle : dans le corps $\mathbb{Z}/3\mathbb{Z}$ , la factorielle

qui vaut

vaut tout simplement 0 puisque

est divisible par

. C'est pourquoi ce théorème nécessite une restriction technique : j'ai choisi de l'énoncer pour des polynômes à coefficients complexes. Les lecteurs qui souhaiteraient utiliser ce cours comme référence (soyons fous) et le relire dans quelques années (idem) noteront que la «bonne» hypothèse est plutôt d'être en caractéristique nulle (quand ils sauront ce que signifie cette hypothèse, ce qui n'est pas encore notre cas).

Théorème 4 Soit un polynôme de $\mathbb{C}[X]$ de degré inférieur ou égal à , et soit un élément de $\mathbb{C}$ . Alors :

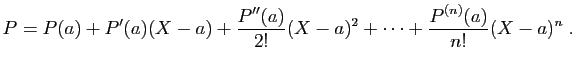
$\displaystyle P=P(a)+{P'(a)}(X-a)+\frac{P'' (a)}{2!}(X-a)^2+ \cdots+\frac{P^{(n)}(a)}{n!}(X-a)^n\;.$

Démonstration : On va travailler dans l'espace vectoriel $\mathbb{C}_n[X]$ et considérer dans cet espace le système $(1,X-a,(X-a)^2,\ldots,(X-a)^n)$ . Ces polynômes sont de degrés successifs $0<1<\cdots<n$ donc on peut appliquer le lemme mis là tout exprès dans les observations d'algèbre linéaire et conclure que c'est un système libre dans $\mathbb{C}_n[X]$ . Voilà une famille de

vecteurs dans un espace de dimension

, c'en est donc une base, et en particulier un système générateur.

$\displaystyle (**)\qquad P'=c_1+2c_2(X-a)+3c_3(X-a)^2\cdots+nc_n(X-a)^{n-1}.$

$\displaystyle (***)\qquad P'' =c_2+6c_3(X-a)+(4\times 3)c_3(X-a)^2\cdots+n(n-1)c_n(X-a)^{n-2}.$

En écrivant formellement une récurrence on montre ainsi que pour tout

avec $1\leqslant k\leqslant n$ , $P^{(k)}(a)=k! c_k$ .

Comme on est dans $\mathbb{C}$ , on peut diviser par

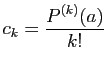et obtenir les relations $c_k=\displaystyle\frac{P^{(k)}(a)}{k!}$ donc la formule annoncée. $\square$

Remarque : On a énoncé ce théorème pour des polynômes à coefficients complexes. Mais si on a par exemple affaire à un polynôme réel, c'est en particulier un polynôme complexe et la formule est donc parfaitement vraie pour ce polynôme aussi.

De cette formule, on peut tirer un énoncé un peu technique sur les racines multiples.

Proposition 14 Soit un polynôme de $\mathbb{C}[X]$ , un nombre complexe et un entier supérieur ou égal à . Alors est une racine au moins -ième de si et seulement si $P(a)=P'(a)=\ldots=P^{(k)}(a)=0$ .

Démonstration : Si

est nul, c'est évident, sinon notons

le degré de

et $\lambda$ son coefficient dominant.

Considérons les indices $i\geqslant 0$ tels que $P^{(i)}(a)\not=0$ , en convenant que $P^{(0)}=P$ . Il existe de tels indices, car le polynôme $P^{(n)}$ est égal à la constante $n! \lambda$ , donc n'est pas nul en

. Cet ensemble non vide d'entiers positifs a donc un plus petit élément

, qui vérifie $0\leqslant m\leqslant n$ . Écrivons la formule de Taylor en mettant en relief cet entier

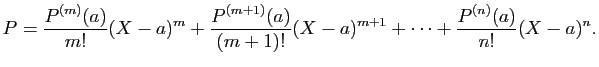
$\displaystyle P=\frac{P^{(m)}(a)}{m!}(X-a)^m+\frac{P^{(m+1)}(a)}{(m+1)!}(X-a)^{m+1}+\cdots+ \frac{P^{(n)}(a)}{n!}(X-a)^n.$

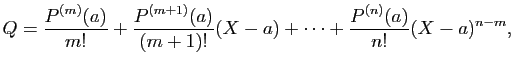
$\displaystyle Q=\frac{P^{(m)}(a)}{m!}+\frac{P^{(m+1)}(a)}{(m+1)!}(X-a)+\cdots+ \frac{P^{(n)}(a)}{n!}(X-a)^{n-m},$

Dès lors,

est racine au moins

-ième de

si et seulement si

, et par définition de

ceci arrive bien si et seulement si $P(a)=P'(a)=\ldots=P^{(k)}(a)=0$ . $\square$