Division suivant les puissances croissantes

Beaucoup moins fondamentale que la division euclidienne, c'est une technique utile pour produire des algorithmes dans des cadres assez variés.

Proposition 19 Soit $\mathbb{K}$ un corps commutatif, et deux polynômes de $\mathbb{K}[X]$ et $n\ge 0$ un entier fixé. On suppose que $B(0)\not=0$ .

Alors il existe un couple unique (de polynômes) vérifiant la double condition :

$\displaystyle A=BQ_n+X^{n+1} S_n\qquad{\rm et}\qquad \deg Q_n \le n.$

Démonstration : La démonstration d'existence n'est pas passionnante (simple description abstraite de l'algorithme de calcul) ; la démonstration d'unicité est plus agréable.

$\bullet$ Pour

, on note

, puis on pose $Q_0=\displaystyle{a_0/b_0}$ (qui existe puisque $B(0)\not=0$ ). On constate alors que

est par construction un polynôme sans terme constant, donc dans lequel

se factorise ; on peut donc mettre

sous la forme

$\bullet$ Soit

fixé et supposons le théorème vrai pour tous polynômes et tout $i\le n$ ; montrons le pour les polynômes

de l'énoncé et pour l'entier

. Commençons par effectuer la division suivant les puissances croissantes de

par

à l'ordre

, et écrivons donc $A=BQ_n+X^{n+1} S_n$ (avec $\deg Q_n \le n$ ), puis effectuons la division suivant les puissances croissantes de

par

à l'ordre 0 : on obtient une constante

et un polynôme

tels que

. On conclut que $A=BQ_n+kBX^{n+1}+X^{n+2}T$ et donc qu'on peut prendre $Q_{n+1}=Q_n+kX^{n+1}$ et $S_{n+1}=T$ pour répondre à la question.

Supposons qu'on ait deux écritures $A=BQ_n^{(1)}+X^{n+1} S_n^{(1)}$ et $A=BQ_n^{(2)}+X^{n+1} S_n^{(2)}$ remplissant les conditions $\deg Q_n^{(1)}\le n$ et $\deg Q_n^{(2)}\le n$ .

Posons alors $Q_n=Q_n^{(1)}-Q_n^{(2)}$ et $S_n=S_n^{(1)}-S_n^{(2)}$ de telle sorte que $0=BQ_n+X^{n+1} S_n$ (obtenue en soustrayant les deux écritures de

) avec en outre la condition $\deg Q_n \le n$ . Comme on a supposé $B(0)\not=0$ ,

ne figure pas parmi les facteurs irréductibles de

, donc $X^{n+1}$ est premier avec

. Mais d'après l'identité $BQ_n=-X^{n+1} S_n$ , $X^{n+1}$ divise

: on en déduit donc que $X^{n+1}$ divise

(lemme de Gauss) ; vu la condition sur le degré de

, ceci entraîne que

= 0. Dès lors $0=X^{n+1} S_n$ donc

. Les deux écritures fournies de

étaient donc la même. $\square$ La division selon les puissances croissantes s'effectue comme la division euclidienne, mais à l'envers : on fait disparaître un par un les termes de plus bas degré du dividende, en multipliant le diviseur par la quantité appropriée. Contrairement à la division euclidienne, on peut la continuer indéfiniment : on ne s'arrête que quand l'ordre désiré est atteint. Par exemple, pour diviser

par

, on écrit :

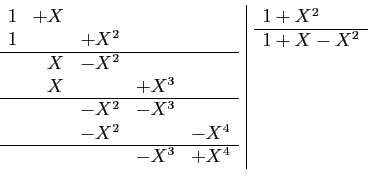
$\begin{displaymath} \begin{array}{l\vert l} \begin{array}{rrrrr} 1&+X&&&\\ 1&&+... ...\ \hline 1+X-X^2\\ \\ \\ \\ \\ \\ \end{array}\end{array}\end{displaymath}$

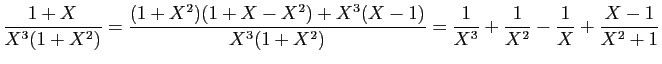
$\displaystyle \frac{1+X}{X^3(1+X^2)} = \frac{(1+X^2)(1+X-X^2)+X^3(X-1)}{X^3(1+X^2)} =\frac{1}{X^3}+\frac{1}{X^2}-\frac{1}{X}+\frac{X-1}{X^2+1}$