-

- Si le degré de
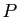 est
est 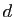 , alors le degré de
, alors le degré de  est
strictement inférieur à
est
strictement inférieur à 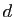 .
.
-
- Si le degré de
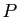 est
est 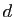 , alors le degré de
, alors le degré de 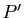 est
est 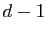 .
.
-
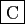
- Si le degré de
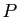 est
est 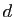 , alors le degré de
, alors le degré de 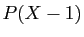 est
est 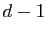 .
.
-
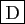
- Si le degré de
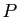 est
est 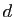 , alors le degré de
, alors le degré de
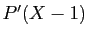 est
est 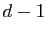 .
.
-
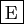
- Si le degré de
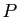 est
est 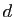 , alors le degré de
, alors le degré de
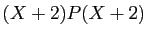 est
est  .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales