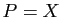 ,
, 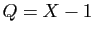
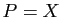 ,
, 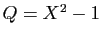
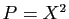 ,
, 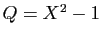
 ,
, 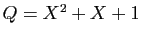
-
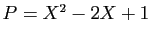 ,
, 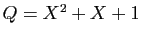
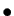
 ,
, 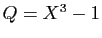
-
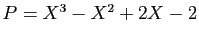 ,
, 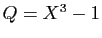
- Écrire les polynômes
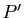 et
et 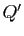 .
.
- Calculer le polynôme
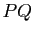 .
.
- Calculer les polynômes
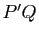 et
et  .
.
- Vérifier la formule
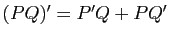
- Calculer les polynômes
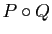 et
et 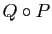 .
.
- Vérifier les formules
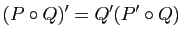 et
et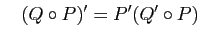
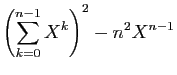
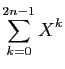 divise
divise
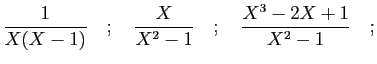
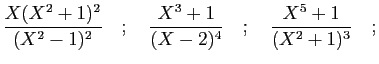
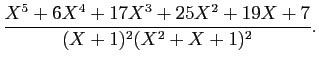
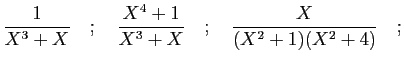
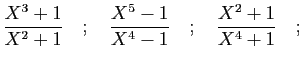
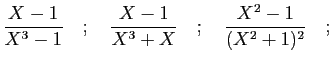
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales