Soit  un espace vectoriel, et
un espace vectoriel, et  un espace affine
de direction
un espace affine
de direction  .
Rappelons que la combinaison linéaire des
.
Rappelons que la combinaison linéaire des 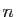 vecteurs
vecteurs
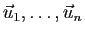 affectés
des
coefficients réels
affectés
des
coefficients réels
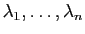 est le vecteur :
est le vecteur :
Passons de l'espace vectoriel à l'espace affine,
c'est-à-dire des vecteurs aux points. Dès qu'une origine  a
été choisie, on peut associer à
a
été choisie, on peut associer à 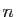 points
points
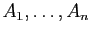 et
et
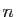 réels
réels
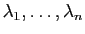 le point
le point 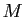 tel que
tel que
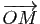 soit la combinaison linéaire :
soit la combinaison linéaire :
La proposition suivante montre que ce point 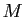 ne dépend pas
du choix de l'origine, quand la somme des coefficients
vaut
ne dépend pas
du choix de l'origine, quand la somme des coefficients
vaut 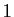 .
.
Démonstration : Il suffit d'utiliser la relation de Chasles:

Vous avez sans doute reconnu dans la proposition
précédente la notion de barycentre d'une famille de points
affectés de coefficients (ou pondérations). Elle vous a
été présentée comme suit.
En remplaçant 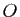 par
par 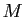 dans (1), on obtient
dans (1), on obtient
Le barycentre 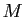 est le seul point de l'espace tel que
la combinaison linéaire des vecteurs
est le seul point de l'espace tel que
la combinaison linéaire des vecteurs
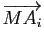 affectés des coefficients
affectés des coefficients 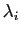 soit nulle.
soit nulle.
Quand les coefficients 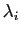 sont tous égaux, on parle
d'isobarycentre. En physique, la notion de barycentre
se réfère à des
coefficients tous positifs, que l'on comprend comme des masses
placées aux points
sont tous égaux, on parle
d'isobarycentre. En physique, la notion de barycentre
se réfère à des
coefficients tous positifs, que l'on comprend comme des masses
placées aux points
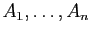 . Le barycentre, ou centre de
gravité, est un point d'équilibre pour l'ensemble des masses.
Insistons sur le fait que dans la définition
8, les coefficients sont de signe quelconque.
. Le barycentre, ou centre de
gravité, est un point d'équilibre pour l'ensemble des masses.
Insistons sur le fait que dans la définition
8, les coefficients sont de signe quelconque.
Proposition 5
Soient 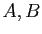 deux points distincts
d'un espace affine. La droite affine passant
par
deux points distincts
d'un espace affine. La droite affine passant
par  et
et 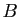 est l'ensemble des barycentres de
est l'ensemble des barycentres de  et
et 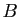 , affectés
de coefficients
, affectés
de coefficients 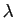 et
et 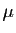 tels que
tels que
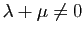 .
.
Démonstration : La droite passant par  et
et 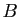 peut être vue comme
la droite passant par
peut être vue comme
la droite passant par  de vecteur directeur
de vecteur directeur
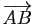 :
:
Soit  une origine quelconque. Le point
une origine quelconque. Le point 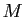 appartient à la droite
appartient à la droite
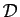 si et seulement si
si et seulement si
pour un certain réel 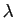 . Donc
. Donc 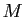 est le barycentre de
est le barycentre de  et
et
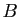 affectés des coefficients
affectés des coefficients
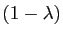 et
et 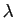 .
Réciproquement, si
.
Réciproquement, si
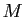 est le barycentre de
est le barycentre de  et
et 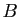 affectés des coefficients
affectés des coefficients
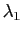 et
et 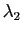 , alors :
, alors :

De façon analogue,
l'ensemble des barycentres de 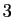 points
est le plan passant par ces
points
est le plan passant par ces 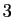 points.
points.
Proposition 6
Soient 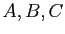 trois points non alignés
d'un espace affine. Le plan affine contenant
trois points non alignés
d'un espace affine. Le plan affine contenant  ,
, 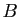 et
et 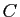 est l'ensemble des barycentres de
est l'ensemble des barycentres de  ,
, 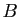 ,
, 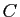 affectés
de coefficients
affectés
de coefficients 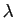 ,
, 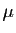 ,
, 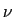 tels que
tels que
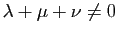 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
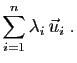
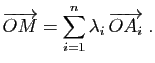
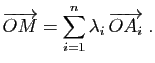
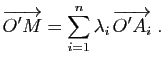
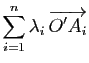
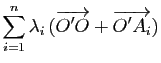
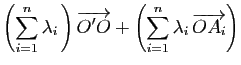
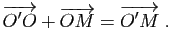
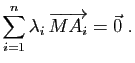
![]() sont tous égaux, on parle
d'isobarycentre. En physique, la notion de barycentre
se réfère à des
coefficients tous positifs, que l'on comprend comme des masses
placées aux points
sont tous égaux, on parle
d'isobarycentre. En physique, la notion de barycentre
se réfère à des
coefficients tous positifs, que l'on comprend comme des masses
placées aux points
![]() . Le barycentre, ou centre de
gravité, est un point d'équilibre pour l'ensemble des masses.
Insistons sur le fait que dans la définition
8, les coefficients sont de signe quelconque.
. Le barycentre, ou centre de
gravité, est un point d'équilibre pour l'ensemble des masses.
Insistons sur le fait que dans la définition
8, les coefficients sont de signe quelconque.
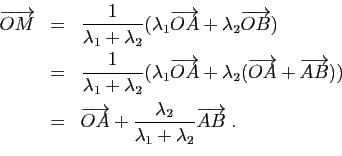
![]() points
est le plan passant par ces
points
est le plan passant par ces ![]() points.
points.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales