Espaces affines

Passons maintenant à la définition d'un espace affine.

Définition 7   Soit $E$ un espace vectoriel sur $\mathbb{R}$. On appelle espace affine de direction $E$ un ensemble ${\cal E}$ non vide, muni d'une application

$$\begin{array}{lcl} {\cal E}\times {\cal E}&\longrightarrow &E\\ (A,B)&\longmapsto&\overrightarrow{AB} \end{array}$$

telle que :

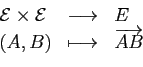
1. pour tout 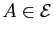$A\in {\cal E}$, l'application qui à 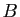$B$ associe 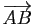$\overrightarrow{AB}$ est bijective: pour tout 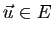$\vec{u}\in E$, il existe un unique 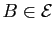$B\in {\cal E}$, tel que 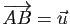$\overrightarrow{AB}=\vec{u}$. On le note $B=A+\vec{u}$ ;
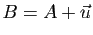2. la relation de Chasles est vérifiée.
   $$\forall A,B,C\in {\cal E}\;,\quad \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\;.$$

Soient $A,C$ deux points de ${\cal E}$, $\vec{u}$ un vecteur de $E$. Notons $B=A+\vec{u}$ et $D=C+\vec{u}$. Les couples de points $(A,B)$ et $(C,D)$ sont dits équipollents: les 4 points $A,B,D,C$ forment un parallélogramme (ses diagonales se coupent en leur milieu: figure 3).

Figure 3: Couples de points équipollents.

La relation d'équipollence est une relation d'équivalence sur l'ensemble ${\cal E}\times {\cal E}$ des couples de points de l'espace affine. À tout vecteur $\vec{u}$ de $E$ correspond une classe d'équivalence de couples et une seule:

$$\vec{u} \longleftrightarrow \{ (A,B)\in {\cal E}\times {\cal E} ,\; B=A+\vec{u} \}\;.$$

Ceci définit une bijection entre l'ensemble quotient de ${\cal E}\times {\cal E}$ par la relation d'équipollence, et l'espace vectoriel associé $E$.

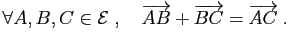
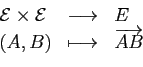
À tout vecteur correspond une classe d'équivalence de couples de points équipollents. Etant donné un couple de points $(A,B)$, le vecteur $\overrightarrow{AB}$ peut donc être interprété comme la classe d'équivalence de $(A,B)$ pour la relation d'équipollence.