Nous donnons ici, sans démonstrations, un résumé (trop) rapide
de la théorie des espaces vectoriels de dimension finie. Ces notions
seront reprises en détail dans un autre chapitre.
Un espace vectoriel est un ensemble sur lequel sont définies ;
- une addition interne (on peut ajouter entre eux deux éléments de
l'ensemble),
- une multiplication externe (on peut multiplier un élément de
l'ensemble par un nombre réel).
Ces deux opérations doivent vérifier certaines
propriétés de compatibilité
qui sont listées dans la définition 1.
Pour la multiplication externe, l'ensemble des
réels peut être remplacé par n'importe quel ensemble de nombres
muni d'une addition et d'une multiplication
(par exemple
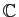 ), sans changer aucun des énoncés qui suivent.
), sans changer aucun des énoncés qui suivent.
Définition 1
Soit  un ensemble non vide.
On dit que
un ensemble non vide.
On dit que  est un espace vectoriel sur
est un espace vectoriel sur
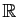 si
si  est muni d'une
addition et d'une multiplication externe vérifiant les
propriétés suivantes.
est muni d'une
addition et d'une multiplication externe vérifiant les
propriétés suivantes.
- Addition:
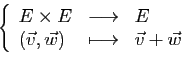
- Associativité:
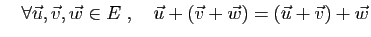
- Élément neutre:
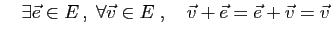
- Opposé:
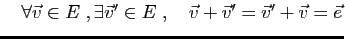
- Commutativité:
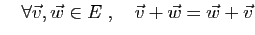
Ces propriétés font de  un groupe commutatif.
un groupe commutatif.
- Multiplication externe:
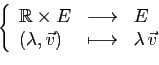
- 5.
- Associativité:
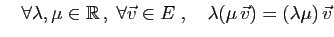
- 6.
- Élément neutre:
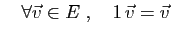
- 7.
- Distributivité (1):
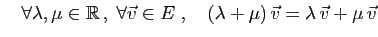
- 8.
- Distributivité (2):
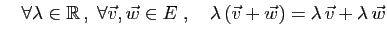
En utilisant les propriétés de la définition, on démontre que :
- le produit par le réel 0 d'un vecteur
 quelconque est
l'élément neutre pour l'addition:
quelconque est
l'élément neutre pour l'addition:
- le produit par le réel
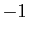 d'un vecteur
d'un vecteur
 quelconque est
son opposé pour l'addition:
quelconque est
son opposé pour l'addition:
En conséquence, on note 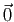 l'élément neutre
pour l'addition (qu'on appelle le vecteur nul) et
l'élément neutre
pour l'addition (qu'on appelle le vecteur nul) et
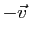 l'opposé de
l'opposé de  .
L'exemple fondamental est l'ensemble des
.
L'exemple fondamental est l'ensemble des
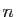 -uplets de réels:
-uplets de réels:
L'ensemble des 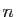 -uplets de réels (couples pour
-uplets de réels (couples pour 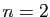 ,
triplets pour
,
triplets pour 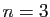 , ...), est muni de l'addition et
de la multiplication par un réel, coordonnée par coordonnée.
, ...), est muni de l'addition et
de la multiplication par un réel, coordonnée par coordonnée.
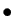
- Addition:
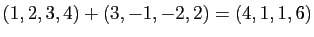
- Multiplication externe:
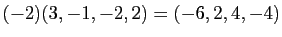
Le singleton contenant seulement le vecteur nul est un espace
vectoriel particulier, dont on convient qu'il est de dimension 0. Tous
les espaces vectoriels considérés dans la suite sont supposés
contenir au moins un vecteur non nul.
La notion de combinaison linéaire,
que nous avons rappelée dans le
cas de deux vecteurs, est l'outil de base des espaces vectoriels.
Dans tout ce qui suit, 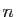 désigne un entier strictement positif.
Une combinaison linéaire de
désigne un entier strictement positif.
Une combinaison linéaire de 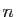 vecteurs se définit comme suit.
vecteurs se définit comme suit.
Un sous-espace d'un espace vectoriel  est un sous-ensemble
qui est lui-même un espace vectoriel pour les opérations de
est un sous-ensemble
qui est lui-même un espace vectoriel pour les opérations de
 . Pour qu'un sous-ensemble soit un sous-espace, il est nécessaire
et suffisant qu'il contienne toutes les combinaisons linéaires d'un
nombre quelconque de ses vecteurs.
. Pour qu'un sous-ensemble soit un sous-espace, il est nécessaire
et suffisant qu'il contienne toutes les combinaisons linéaires d'un
nombre quelconque de ses vecteurs.
Définition 3
Soit  un espace vectoriel,
un espace vectoriel, 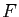 un sous-ensemble de
un sous-ensemble de  . On appelle
sous-espace engendré par
. On appelle
sous-espace engendré par 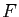 l'ensemble des combinaisons
linéaires de vecteurs de
l'ensemble des combinaisons
linéaires de vecteurs de 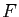 .
.
Tout sous-espace contenant 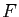 , contient nécessairement
le sous-espace engendré par
, contient nécessairement
le sous-espace engendré par 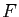 .
.
Deux vecteurs liés sont colinéaires, trois
vecteurs liés sont dits coplanaires.
Rappelons que deux vecteurs  et
et  sont colinéaires
si et seulement s'il existe un nombre réel
sont colinéaires
si et seulement s'il existe un nombre réel 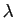 tel que
tel que
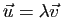 ou
ou
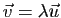 .
Plus généralement, si
.
Plus généralement, si 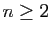 , une famille
, une famille
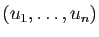 est liée
si et seulement s'il existe
est liée
si et seulement s'il existe
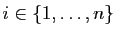 tels que
tels que
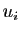 soit combinaison linéaire de la famille
soit combinaison linéaire de la famille
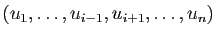 .
.
Théorème 1
Dans un espace vectoriel de dimension finie, contenant des vecteurs
non nuls, il existe une infinité de bases et
toutes les bases ont le
même cardinal.
Par définition,
le nombre d'éléments commun de toutes les bases est la
dimension de l'espace.
Les coordonnées d'un vecteur sont définies grâce au
résultat suivant.
Les réels
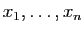 sont les
coordonnées de
sont les
coordonnées de  dans la base
dans la base
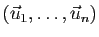 .
Le
.
Le 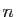 -uplet
-uplet
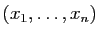 est un élément de l'espace
vectoriel
est un élément de l'espace
vectoriel
 . Dans
. Dans
 , la
base la plus naturelle est constituée des
, la
base la plus naturelle est constituée des 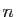 -uplets dont une seule
coordonnée vaut
-uplets dont une seule
coordonnée vaut 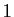 , les autres étant nulles.
, les autres étant nulles.
On appelle cette base, la base canonique.
Constatez avec soulagement que les coordonnées du 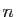 -uplet
-uplet
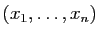 dans la base canonique sont les
dans la base canonique sont les 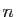 réels
réels
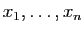 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
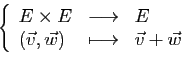
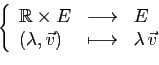
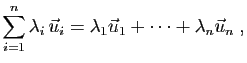
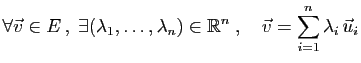
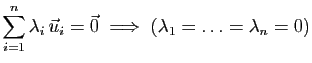
![]() et
et ![]() sont colinéaires
si et seulement s'il existe un nombre réel
sont colinéaires
si et seulement s'il existe un nombre réel ![]() tel que
tel que
![]() ou
ou
![]() .
Plus généralement, si
.
Plus généralement, si ![]() , une famille
, une famille
![]() est liée
si et seulement s'il existe
est liée
si et seulement s'il existe
![]() tels que
tels que
![]() soit combinaison linéaire de la famille
soit combinaison linéaire de la famille
![]() .
.
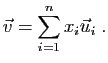
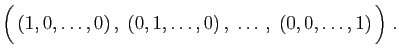
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales