Une des difficultés de la géométrie
est de bien comprendre la différence entre
les points et les vecteurs. On vous a appris que les points sont
«fixés» et les vecteurs sont «libres»
(d'être translatés n'importe où dans le plan ou dans l'espace).
Cette vision des choses est largement suffisante pour vous permettre
d'effectuer des calculs, et vous pouvez vous en contenter pour
l'instant. Nous décrirons à la section suivante le formalisme
mathématique de ces notions.
Un espace vectoriel est un ensemble de vecteurs muni de deux
opérations, l'addition et la multiplication par un réel. Ce sont
bien celles que vous connaissez et leurs propriétés
vous sont familières (figure 1).
Figure 1:
Addition de deux vecteurs et multiplication d'un vecteur par
un réel.
|
|
L'addition et la multiplication par un réel induisent la notion de
combinaison linéaire. Si 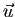 et
et
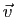 sont deux vecteurs, les combinaisons linéaires
de
sont deux vecteurs, les combinaisons linéaires
de 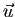 et
et 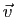 sont les vecteurs de la forme
sont les vecteurs de la forme
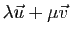 , où
, où 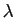 et
et
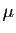 sont deux réels quelconques.
On dit que
sont deux réels quelconques.
On dit que 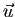 et
et 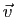 sont liés si une de leurs
combinaisons linéaires est égale au vecteur nul (noté
sont liés si une de leurs
combinaisons linéaires est égale au vecteur nul (noté
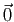 ) sans que les coefficients
) sans que les coefficients 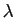 et
et 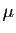 soient tous les deux nuls. C'est équivalent à dire que l'un des
deux vecteurs est égal au produit de l'autre par un réel : on dit
aussi que les deux vecteurs sont colinéaires.
soient tous les deux nuls. C'est équivalent à dire que l'un des
deux vecteurs est égal au produit de l'autre par un réel : on dit
aussi que les deux vecteurs sont colinéaires.
Une droite vectorielle est un espace vectoriel contenant des
vecteurs non nuls, dans lequel tous les vecteurs sont colinéaires
entre eux. Dans une droite vectorielle tout vecteur non nul constitue
une base. Soit 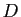 une droite vectorielle et
une droite vectorielle et
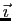 une base de
une base de 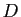 . Pour tout
vecteur
. Pour tout
vecteur 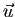 de
de 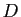 , il existe un réel
, il existe un réel
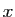 unique tel que
unique tel que
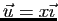 .
.
Un plan
vectoriel est un espace vectoriel contenant deux vecteurs non
colinéaires, et dans lequel tout vecteur
est combinaison linéaire de ces deux
vecteurs. Soit 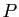 un plan vectoriel.
Tout couple de vecteurs de
un plan vectoriel.
Tout couple de vecteurs de 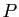 non colinéaires est
une base du plan vectoriel.
Soit
non colinéaires est
une base du plan vectoriel.
Soit
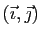 une base de
une base de
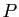 . À tout vecteur
. À tout vecteur 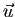 de
de
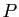 correspond un
couple unique de réels
correspond un
couple unique de réels
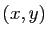 tel que
tel que
Les deux réels 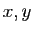 sont les coordonnées du vecteur
sont les coordonnées du vecteur
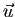 dans la base
dans la base
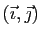 .
.
L'addition et la multiplication des vecteurs se traduisent par les
mêmes opérations sur les coordonnées.
Soit 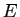 un espace vectoriel. Un espace
affine
un espace vectoriel. Un espace
affine  est un ensemble de points.
On suppose définie une application de
est un ensemble de points.
On suppose définie une application de
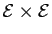 vers
vers
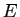 , qui à un couple
, qui à un couple 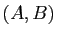 associe un vecteur,
noté
associe un vecteur,
noté
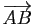 .
Voyez le couple
.
Voyez le couple 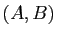 comme une localisation dans l'espace
affine du vecteur,
comme une localisation dans l'espace
affine du vecteur, 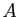 étant
l'origine et
étant
l'origine et 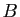 l'extrémité.
Au sens de l'addition des vecteurs, la
relation suivante, dite relation de Chasles, est vraie pour tous
points
l'extrémité.
Au sens de l'addition des vecteurs, la
relation suivante, dite relation de Chasles, est vraie pour tous
points 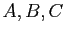 de l'espace affine
de l'espace affine  .
.
Si de plus pour tout 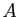 , l'application de
, l'application de  vers
vers 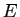 qui à
qui à 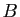 associe
associe
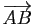 est bijective, on dit que
l'espace vectoriel
est bijective, on dit que
l'espace vectoriel 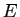 et l'espace affine
et l'espace affine  sont
associés, ou bien que
sont
associés, ou bien que  est dirigé par
est dirigé par
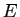 .
Lorsque
.
Lorsque
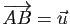 , on écrit :
, on écrit :
malgré le risque de confusion avec l'addition des vecteurs. Cet abus
de notation sera justifié plus loin.
Soit 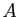 un point d'un espace affine
un point d'un espace affine  ,
, 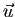 un vecteur
non nul de
un vecteur
non nul de 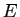 , et
, et
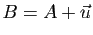 .
.
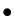
- La droite affine passant par
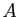 et
et
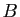 est
l'ensemble des points
est
l'ensemble des points 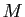 tels que
tels que
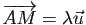 , quand
, quand 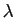 parcourt
parcourt
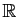 .
.
- Le segment
![$ [A,B]$](img40.gif) est
l'ensemble des points
est
l'ensemble des points 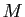 tels que
tels que
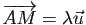 , quand
, quand 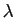 parcourt l'intervalle
parcourt l'intervalle ![$ [0,1]$](img41.gif) .
.
- Le milieu du segment
![$ [A,B]$](img40.gif) est
le point
est
le point 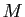 tel que
tel que
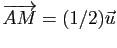 .
.
La droite vectorielle
est associée à la droite affine
Le plan vectoriel
est associé au plan affine
Dans le plan,
deux droites affines sont dirigées
par une même droite vectorielle si et seulement si
elles sont parallèles (d'intersection vide) ou confondues. Par un
point donné, passe une unique droite dont un vecteur directeur est
donné, et donc une unique parallèle à une droite donnée : c'est
le fameux cinquième postulat d'Euclide.
Il est possible de choisir une même origine 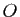 pour les
représentants de tous les vecteurs: à chaque vecteur
pour les
représentants de tous les vecteurs: à chaque vecteur
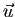 on associe alors l'unique point
on associe alors l'unique point 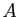 tel que
tel que
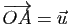 . On définit ainsi une
bijection de l'ensemble des vecteurs vers l'ensemble des points.
. On définit ainsi une
bijection de l'ensemble des vecteurs vers l'ensemble des points.
Si
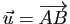 ,
la relation de Chasles justifie la notation
,
la relation de Chasles justifie la notation
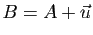 ,
puisqu'alors
,
puisqu'alors
au sens de l'addition des vecteurs.
La donnée d'une origine 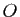 et d'une base
de l'espace vectoriel
et d'une base
de l'espace vectoriel
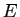 constitue un repère de l'espace affine
associé:
tout point
constitue un repère de l'espace affine
associé:
tout point 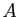 de
de  est repéré de façon unique par les
coordonnées du vecteur
est repéré de façon unique par les
coordonnées du vecteur
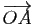 dans la base. Par
exemple si le plan affine
dans la base. Par
exemple si le plan affine 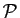 est muni d'un repère
est muni d'un repère
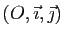 ,
à tout point
,
à tout point 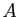 du plan correspond le couple unique de réels
du plan correspond le couple unique de réels
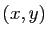 qui sont les coordonnées du vecteur
qui sont les coordonnées du vecteur
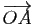 dans la base
dans la base
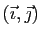 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![\includegraphics[width=7cm]{additionvecteurs}](img3.gif)
![]() une droite vectorielle et
une droite vectorielle et
![]() une base de
une base de ![]() . Pour tout
vecteur
. Pour tout
vecteur ![]() de
de ![]() , il existe un réel
, il existe un réel
![]() unique tel que
unique tel que
![]() .
.
![]() un plan vectoriel.
Tout couple de vecteurs de
un plan vectoriel.
Tout couple de vecteurs de ![]() non colinéaires est
une base du plan vectoriel.
Soit
non colinéaires est
une base du plan vectoriel.
Soit
![]() une base de
une base de
![]() . À tout vecteur
. À tout vecteur ![]() de
de
![]() correspond un
couple unique de réels
correspond un
couple unique de réels
![]() tel que
tel que
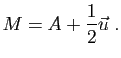
![]() pour les
représentants de tous les vecteurs: à chaque vecteur
pour les
représentants de tous les vecteurs: à chaque vecteur
![]() on associe alors l'unique point
on associe alors l'unique point ![]() tel que
tel que
![]() . On définit ainsi une
bijection de l'ensemble des vecteurs vers l'ensemble des points.
. On définit ainsi une
bijection de l'ensemble des vecteurs vers l'ensemble des points.
![]() ,
la relation de Chasles justifie la notation
,
la relation de Chasles justifie la notation
![]() ,
puisqu'alors
,
puisqu'alors
![]() et d'une base
de l'espace vectoriel
et d'une base
de l'espace vectoriel
![]() constitue un repère de l'espace affine
associé:
tout point
constitue un repère de l'espace affine
associé:
tout point ![]() de
de ![]() est repéré de façon unique par les
coordonnées du vecteur
est repéré de façon unique par les
coordonnées du vecteur
![]() dans la base. Par
exemple si le plan affine
dans la base. Par
exemple si le plan affine ![]() est muni d'un repère
est muni d'un repère
![]() ,
à tout point
,
à tout point ![]() du plan correspond le couple unique de réels
du plan correspond le couple unique de réels
![]() qui sont les coordonnées du vecteur
qui sont les coordonnées du vecteur
![]() dans la base
dans la base
![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales