Les Éléments sont un traité mathématique et
géométrique, constitué de 13 livres organisés
thématiquement, probablement écrit par Euclide vers 300 avant
J.-C. Il comprend une collection de définitions, axiomes,
théorèmes et démonstrations sur la géométrie et les nombres.
C'est le plus ancien exemple connu d'un traitement axiomatique et
systématique de la géométrie et son influence sur le
développement de la science occidentale est fondamentale. Il s'agit
du livre de mathématiques le plus lu au cours
de l'histoire : les Éléments furent l'un des premiers livres
imprimés et ont connu depuis plus de 1000 éditions.
Pendant des siècles, vos prédecesseurs ont
appris les mathématiques non pas dans des polycopiés, mais dans les
Éléments.
Le livre I contient 5
postulats de géométrie plane.
- Un segment de droite peut être tracé en joignant deux points
quelconques.
- Un segment de droite peut être prolongé indéfiniment en une
ligne droite.
- Etant donné un segment de droite quelconque, un cercle peut être
tracé en prenant ce segment comme rayon et l'une de ses
extrémités comme centre.
- Tous les angles droits sont congruents
- Si deux droites sont sécantes avec une troisième de telle façon
que la somme des angles intérieurs d'un côte soit inférieure à
deux angles droits, alors ces deux droites sont forcément sécantes
de ce côté.
La contraposée du cinquième postulat est que si deux droites ne se
coupent pas, alors la somme des angles intérieurs à toute
sécante est égale à 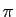 . En conséquence, par un point
donné, il ne peut passer qu'une parallèle à une droite donnée.
. En conséquence, par un point
donné, il ne peut passer qu'une parallèle à une droite donnée.
Pour cette raison, le cinquième postulat s'appelle le postulat des
parallèles. Il a toujours semblé moins évident
que les autres, et de nombreux mathématiciens ont pensé qu'il pouvait
être démontré à partir des précédents.
Pendant des siècles,
toutes les tentatives échouèrent. La plupart d'entre elles
étaient des essais de
démonstration par l'absurde. Nombreux furent ceux qui conclurent à
une contradiction devant ce qu'ils percevaient comme une
impossibilité «évidente» mais qui n'était nullement une
contradiction mathématique. Parmi ces courageux, Giovanni Saccheri
(1667-1733) mérite une mention spéciale. En 1733, il publie
«Euclides ab omni naevo vindicatus» (Euclide lavé de toute
tache).
Partant du postulat que par un point on peut faire passer une infinité de
droites distinctes qui ne coupent pas une droite donnée, Saccheri
démontre quantité de théorèmes, et devant leur évidente
bizarrerie, conclut qu'il a démontré par l'absurde le cinquième
postulat d'Euclide.
Figure 15:
Le disque de Poincaré : modèle de la géométrie
hyperbolique.
|
|
Pourtant, les résultats de Saccheri sont maintenant des théorèmes connus
de la géométrie hyperbolique. Ce n'est qu'au XIXe
siècle que Lobachevski, Boliaï, et sans doute Gauss, reconnurent
qu'il était impossible de démontrer le cinquième
postulat d'Euclide : on obtient simplement des géométries
différentes avec des postulats
différents.
- par un point ne passe aucune parallèle à une droite donnée :
géométrie sphérique
- par un point passe exactement une parallèle à une droite donnée :
géométrie euclidienne
- par un point passe une infinité de parallèles à une droite donnée :
géométrie hyperbolique
Parmi les conséquences, la somme des angles d'un triangle, qui vaut
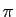 en géométrie euclidienne, est supérieure à
en géométrie euclidienne, est supérieure à 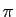 en
géométrie sphérique, et inférieure à
en
géométrie sphérique, et inférieure à 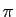 en géométrie
hyperbolique. Voici l'expression du théorème d'Al-Kashi
4 dans les
trois géométries.
en géométrie
hyperbolique. Voici l'expression du théorème d'Al-Kashi
4 dans les
trois géométries.
- géométrie sphérique :
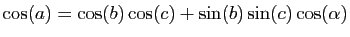
- géométrie euclidienne :
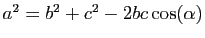
- géométrie hyperbolique :
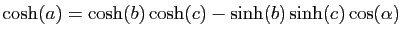
La géométrie sphérique est facile à visualiser : sur une
sphère en dimension 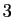 , il suffit de baptiser «droite» tout cercle
de rayon maximal (intersection de la sphère avec un plan passant par
le centre). La géométrie hyperbolique est moins facile à
imaginer. Henri Poincaré (1854-1912) a proposé deux modèles
équivalents. Dans le premier, les points sont ceux d'un demi-plan
de la géométrie euclidienne, mais on appelle «droite»
les demi-cercles centrés sur l'axe des abscisses. Dans le second,
les points sont ceux d'un disque, et les «droites» sont les
arcs de cercle qui coupent orthogonalement le cercle bordant le disque. La
figure 15 montre des droites hyperboliques, soit
orthogonales deux à deux, soit parallèles. Elles forment des
«triangles» rectangles dont deux côtés sont infinis et deux angles
nuls.
, il suffit de baptiser «droite» tout cercle
de rayon maximal (intersection de la sphère avec un plan passant par
le centre). La géométrie hyperbolique est moins facile à
imaginer. Henri Poincaré (1854-1912) a proposé deux modèles
équivalents. Dans le premier, les points sont ceux d'un demi-plan
de la géométrie euclidienne, mais on appelle «droite»
les demi-cercles centrés sur l'axe des abscisses. Dans le second,
les points sont ceux d'un disque, et les «droites» sont les
arcs de cercle qui coupent orthogonalement le cercle bordant le disque. La
figure 15 montre des droites hyperboliques, soit
orthogonales deux à deux, soit parallèles. Elles forment des
«triangles» rectangles dont deux côtés sont infinis et deux angles
nuls.
Figure:
«Limite circulaire» de M.C. Escher.
|
|
Les triangles de la figure 15
constituent un pavage du plan hyperbolique. Les
possibilités pour paver le plan hyperbolique sont beaucoup plus
étendues qu'en géométrie euclidienne : on peut par exemple
utiliser des pavés à 4 côtés dont deux angles opposés
valent 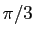 , et les deux autres
, et les deux autres 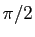 : ce
pavage est illustré par la figure 16. Le
peintre hollandais M.C. Escher était fasciné par la symétrie et
l'infini mais il ne connaissait pas les mathématiques quand il a
réalisé cette gravure.
Après avoir vu ses
: ce
pavage est illustré par la figure 16. Le
peintre hollandais M.C. Escher était fasciné par la symétrie et
l'infini mais il ne connaissait pas les mathématiques quand il a
réalisé cette gravure.
Après avoir vu ses  uvres, le mathématicien H.S.M. Coxeter
demanda à le rencontrer, et lui expliqua qu'il avait
réinventé les pavages du plan hyperbolique.
uvres, le mathématicien H.S.M. Coxeter
demanda à le rencontrer, et lui expliqua qu'il avait
réinventé les pavages du plan hyperbolique.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales