-
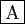
- La droite passant par
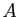 de vecteur directeur
de vecteur directeur 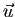 contient les
points
contient les
points 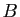 et
et 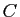 .
.
-
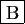
- Il existe une unique droite passant par
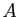 et de vecteur directeur
et de vecteur directeur
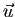 .
.
-
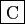
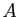 est le milieu du segment
est le milieu du segment ![$ [B,C]$](img482.gif) .
.
-
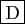
- Il existe un unique plan passant par les trois points
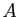 ,
, 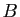 et
et 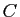 .
.
-
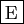
- Le vecteur
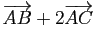 est un vecteur
directeur de la droite
est un vecteur
directeur de la droite 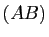 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales