Nous définissons d'abord les
outils de base de l'approximation que sont la valeur absolue, la
distance et la partie entière.
La valeur absolue d'un réel  , notée
, notée 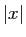 ,
est
,
est
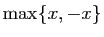 . Elle est
égale à
. Elle est
égale à  si
si  est positif,
est positif, 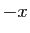 si
si  est négatif.
est négatif.
Si  et
et 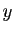 sont deux réels quelconques, la valeur absolue du
produit
sont deux réels quelconques, la valeur absolue du
produit 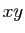 est le produit des valeurs absolues ;
est le produit des valeurs absolues ;
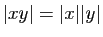 . Par
contre, on peut seulement encadrer la valeur absolue de la somme.
. Par
contre, on peut seulement encadrer la valeur absolue de la somme.
Proposition 5
Soient  et
et 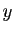 deux réels quelconques.
La valeur absolue de leur somme
est majorée par la somme des valeurs absolues,
et minorée par la différence des valeurs absolues.
deux réels quelconques.
La valeur absolue de leur somme
est majorée par la somme des valeurs absolues,
et minorée par la différence des valeurs absolues.
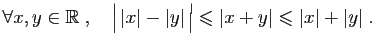 |
(1) |
Démonstration : Quitte à échanger  et
et 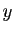 , nous pouvons supposer sans perte de
généralité que
, nous pouvons supposer sans perte de
généralité que
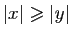 . Si l'un des deux est nul, alors
les inégalités sont vérifiées : ce sont des
égalités. Sinon, il suffit d'examiner les 4 cas possibles selon le
signe de
. Si l'un des deux est nul, alors
les inégalités sont vérifiées : ce sont des
égalités. Sinon, il suffit d'examiner les 4 cas possibles selon le
signe de  et
et 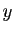 .
.
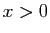 et
et 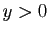 :
:
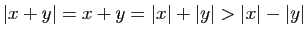
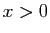 et
et 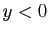 :
:
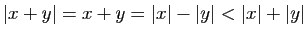
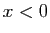 et
et 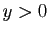 :
:
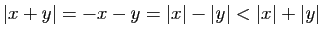
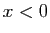 et
et 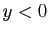 :
:
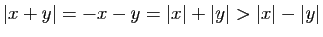
Observez que dans tous les cas, l'une des deux inégalités est une
égalité, mais ce n'est pas toujours la même. En remplaçant
En remplaçant 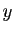 par
par 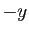 , on obtient le même encadrement pour
la valeur absolue d'une différence.
, on obtient le même encadrement pour
la valeur absolue d'une différence.
On appelle distance entre deux réels  et
et 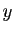 la valeur absolue
de leur différence. La proposition 5,
appliquée à
la valeur absolue
de leur différence. La proposition 5,
appliquée à
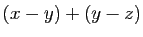 ,
entraîne :
,
entraîne :
Pour aller d'un point à un autre, on ne peut qu'allonger le parcours
si on s'impose de passer par un troisième : c'est l'inégalité
triangulaire.
Étant donné un réel  et un réel
et un réel
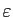 strictement
positif, nous dirons que
strictement
positif, nous dirons que 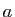 est une approximation
(ou une valeur approchée)
de
est une approximation
(ou une valeur approchée)
de  «à
«à
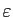 près» si la distance de
près» si la distance de 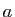 à
à  est
inférieure à
est
inférieure à
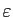 , ce qui équivaut à dire que
, ce qui équivaut à dire que  appartient
à l'intervalle
appartient
à l'intervalle
![$ ]a-\varepsilon ,a+\varepsilon [$](img194.gif) .
.
Les approximations décimales se construisent à l'aide de la partie
entière. La partie entière d'un réel  est le plus grand
entier inférieur ou égal à
est le plus grand
entier inférieur ou égal à  . On le note
. On le note
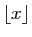 :
:
On en déduit :
La partie entière de 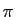 est
est 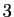 . Attention : la partie entière
de
. Attention : la partie entière
de 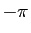 est
est 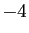 , et non
, et non 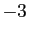 . On appelle partie décimale
de
. On appelle partie décimale
de  et on note
et on note 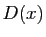 , la différence de
, la différence de  avec sa partie
entière.
avec sa partie
entière.
Soit  un réel, et
un réel, et 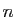 un entier. Considérons la partie
entière de
un entier. Considérons la partie
entière de 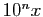 :
:
donc,
Le nombre décimal
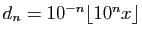 est
l'approximation de
est
l'approximation de  par défaut à
par défaut à 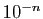 près. Observez que
près. Observez que
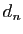 et
et 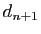 coïncident jusqu'à la dernière décimale de
coïncident jusqu'à la dernière décimale de
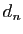 :
:
Par exemple, pour 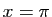 ,
,
Réciproquement, la donnée d'une suite de décimaux
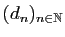 , telle que
, telle que
-
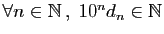
-
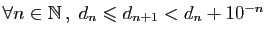
détermine un réel  tel que pour tout
tel que pour tout 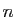
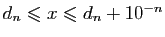 .
La suite
.
La suite
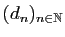 est croissante et converge
vers
est croissante et converge
vers  . Notez
. Notez 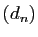 peut déterminer un réel dont elle
n'est pas la suite d'approximations décimales, dans le cas où
peut déterminer un réel dont elle
n'est pas la suite d'approximations décimales, dans le cas où  est lui même décimal :
est lui même décimal :
En théorie, on peut approcher un réel  par un nombre
décimal à n'importe quelle précision. En pratique, la
précision habituelle sur des calculs d'ordinateurs est de l'ordre de
par un nombre
décimal à n'importe quelle précision. En pratique, la
précision habituelle sur des calculs d'ordinateurs est de l'ordre de
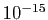 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() , notée
, notée ![]() ,
est
,
est
![]() . Elle est
égale à
. Elle est
égale à ![]() si
si ![]() est positif,
est positif, ![]() si
si ![]() est négatif.
est négatif.
![]() et
et ![]() sont deux réels quelconques, la valeur absolue du
produit
sont deux réels quelconques, la valeur absolue du
produit ![]() est le produit des valeurs absolues ;
est le produit des valeurs absolues ;
![]() . Par
contre, on peut seulement encadrer la valeur absolue de la somme.
. Par
contre, on peut seulement encadrer la valeur absolue de la somme.
![]() et un réel
et un réel
![]() strictement
positif, nous dirons que
strictement
positif, nous dirons que ![]() est une approximation
(ou une valeur approchée)
de
est une approximation
(ou une valeur approchée)
de ![]() «à
«à
![]() près» si la distance de
près» si la distance de ![]() à
à ![]() est
inférieure à
est
inférieure à
![]() , ce qui équivaut à dire que
, ce qui équivaut à dire que ![]() appartient
à l'intervalle
appartient
à l'intervalle
![]() .
.
![]() un réel, et
un réel, et ![]() un entier. Considérons la partie
entière de
un entier. Considérons la partie
entière de ![]() :
:
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales