Rationnels et irrationnels

Un nombre rationnel est le quotient de deux entiers relatifs. La somme de deux rationnels, ainsi que leur produit, sont des rationnels. Muni de l'addition et de la multiplication, $\mathbb{Q}$ est un corps commutatif totalement ordonné, comme $\mathbb{R}$ . En revanche, $\mathbb{Q}$ ne possède pas la propriété de la borne supérieure. L'ensemble des rationnels dont le carré est inférieur ou égal à est non vide, majoré, mais il n'a pas de borne supérieure dans $\mathbb{Q}$ , car $\sqrt{2}$ est irrationnel. C'est une application du résultat suivant.

Proposition 4 Soient et deux entiers strictement positifs. Le nombre $\sqrt[n]{m}$ est soit entier, soit irrationnel.

Démonstration : Nous allons démontrer que si $\sqrt[n]{m}$ est rationnel, alors il est entier. Soient

deux entiers premiers entre eux tels que $\sqrt[n]{m}=p/q$ . Alors,

. Mais alors

divise

, or

sont premiers entre eux. Ce n'est possible que si

. $\square$

Observons que la somme d'un rationnel et d'un irrationnel est irrationnelle ; il en est de même pour leur produit. Par contre la somme ou le produit de deux irrationnels peuvent être rationnels (par exemple $1+\sqrt{2}$ et $1-\sqrt{2}$ ).

Les rationnels et les irrationnels sont intimement mêlés, comme le montre le théorème suivant.

Théorème 2 Si un intervalle de $\mathbb{R}$ contient au moins deux points distincts, il contient au moins un rationnel et un irrationnel.

On traduit cette propriété en disant que $\mathbb{Q}$ et $\mathbb{R}\setminus \mathbb{Q}$ sont denses dans $\mathbb{R}$ . Démonstration : Soit

un intervalle contenant deux points

, tels que

. Soit

un entier strictement supérieur à

le plus petit entier strictement supérieur à

. On a donc :

$\displaystyle p-1\leqslant aq <p\;,$

et comme

est strictement positif,

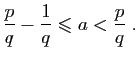
$\displaystyle \frac{p}{q}-\frac{1}{q}\leqslant a<\frac{p}{q}\;.$

D'où :

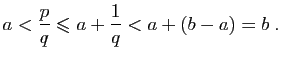
$\displaystyle a<\frac{p}{q}\leqslant a+\frac{1}{q}<a+(b-a)=b\;.$

Donc l'intervalle

, inclus dans

, contient le rationnel $\frac{p}{q}$ .

De même, l'intervalle $]\frac{a}{\sqrt{2}},\frac{b}{\sqrt{2}}[$ contient un rationnel ; donc contient $r\sqrt{2}$ , qui est irrationnel. $\square$

En fait, tout intervalle contenant au moins deux points contient une infinité de rationnels et une infinité d'irrationnels.

Les rationnels que l'on manipule le plus souvent sont les nombres décimaux, qui sont les multiples entiers de $10^{-n}$ , où est le nombre de chiffres après la virgule :

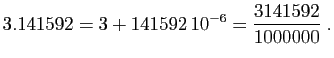
$\displaystyle 3.141592 =3+141592 10^{-6}=\frac{3141592}{1000000}\;.$

Les nombres décimaux sont le moyen le plus courant d'approcher les réels.