On dit qu'un ensemble de réels  admet un
plus grand
élément (respectivement plus petit élément) s'il
existe
admet un
plus grand
élément (respectivement plus petit élément) s'il
existe 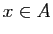 tel que pour tout
tel que pour tout 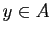 ,
,
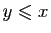 (respectivement :
(respectivement :
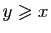 ). Donc le plus grand élément
(s'il existe il est nécessairement unique) est à la fois un
majorant de
). Donc le plus grand élément
(s'il existe il est nécessairement unique) est à la fois un
majorant de  et un élément de
et un élément de  .
Le fait que l'ordre sur
.
Le fait que l'ordre sur
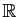 soit total entraîne que tout
ensemble fini de réels admet un plus petit élément
et un plus grand élément. Si
soit total entraîne que tout
ensemble fini de réels admet un plus petit élément
et un plus grand élément. Si
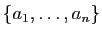 est un
ensemble fini de réels, nous noterons
est un
ensemble fini de réels, nous noterons
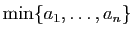 le
plus petit et
le
plus petit et
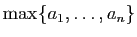 le plus grand élément. Nous
réserverons les notations
le plus grand élément. Nous
réserverons les notations 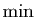 et
et 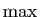 aux ensembles finis. Un
ensemble infini de réels n'admet pas nécessairement de plus
petit ou de plus grand élément. Voici quelques exemples.
aux ensembles finis. Un
ensemble infini de réels n'admet pas nécessairement de plus
petit ou de plus grand élément. Voici quelques exemples.
| Ensemble |
Plus petit élément |
Plus grand élément |
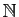 |
0 |
Non |
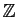 |
Non |
Non |
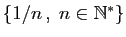 |
Non |
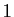 |
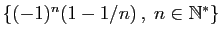 |
Non |
Non |
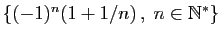 |
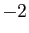 |
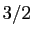 |
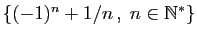 |
Non |
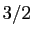 |
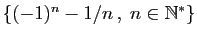 |
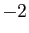 |
Non |
Non seulement
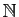 n'a pas de plus grand élément mais de
plus aucun réel n'est plus grand que tous les éléments de
n'a pas de plus grand élément mais de
plus aucun réel n'est plus grand que tous les éléments de
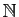 . Par contre, les 5 derniers ensembles du tableau
ci-dessus sont bornés au sens suivant.
. Par contre, les 5 derniers ensembles du tableau
ci-dessus sont bornés au sens suivant.
Définition 2
Soit  une partie de
une partie de
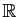 (un ensemble de réels). On dit
que
(un ensemble de réels). On dit
que  est :
est :
- majorée s'il existe un majorant de
 ,
,
- minorée s'il existe un minorant de
 ,
,
- bornée si
 est à la fois majorée et minorée.
est à la fois majorée et minorée.
Si 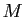 est un majorant de
est un majorant de  , alors
, alors 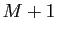 ,
, 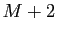 et plus
généralement tout réel plus grand que
et plus
généralement tout réel plus grand que 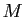 sont aussi des
majorants. Nous admettrons pour l'instant le théorème suivant,
dont nous donnerons une démonstration dans la section 1.6.
sont aussi des
majorants. Nous admettrons pour l'instant le théorème suivant,
dont nous donnerons une démonstration dans la section 1.6.
Théorème 1
Soit  une partie non vide de
une partie non vide de
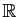 .
.
- Si
 est majorée, alors l'ensemble des majorants de
est majorée, alors l'ensemble des majorants de  admet un
plus petit élément.
admet un
plus petit élément.
- Si
 est minorée, alors l'ensemble des minorants de
est minorée, alors l'ensemble des minorants de  admet un
plus grand élément.
admet un
plus grand élément.
Définition 3
Soit  une partie non vide de
une partie non vide de
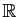 .
.
- Si
 est majorée, on appelle borne supérieure de
est majorée, on appelle borne supérieure de  et on
note
et on
note 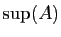 le plus petit des majorants de
le plus petit des majorants de  .
.
- Si
 est minorée, on appelle borne inférieure de
est minorée, on appelle borne inférieure de  et on
note
et on
note 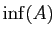 le plus grand des minorants de
le plus grand des minorants de  .
.
Du fait que l'ordre des réels est total, la borne supérieure et la
borne inférieure, si elles existent, sont nécessairement uniques.
Lorsque  admet un plus grand élément, la borne supérieure de
admet un plus grand élément, la borne supérieure de
 est ce plus grand élément.
Lorsque
est ce plus grand élément.
Lorsque  admet un plus petit élément, la borne inférieure de
admet un plus petit élément, la borne inférieure de
 est ce plus petit élément.
On étend la définition de
est ce plus petit élément.
On étend la définition de 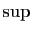 et
et 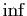 aux ensembles non
majorés et non minorés par la convention suivante.
aux ensembles non
majorés et non minorés par la convention suivante.
- Si
 n'est pas majorée,
n'est pas majorée,
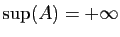
- Si
 n'est pas minorée,
n'est pas minorée,
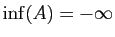
Reprenons comme exemples les 6 ensembles du tableau précédent.
| Ensemble |
Borne inférieure |
Borne supérieure |
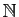 |
0 |
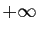 |
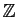 |
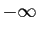 |
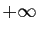 |
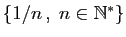 |
0 |
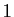 |
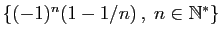 |
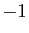 |
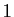 |
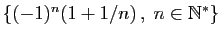 |
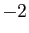 |
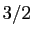 |
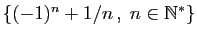 |
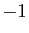 |
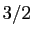 |
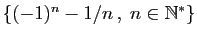 |
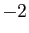 |
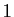 |
Dans le cas où  est majorée et n'admet pas de plus grand
élément, alors
est majorée et n'admet pas de plus grand
élément, alors 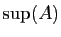 n'appartient pas à
n'appartient pas à  , mais on trouve
néanmoins des éléments de
, mais on trouve
néanmoins des éléments de  arbitrairement proches de la borne
supérieure.
arbitrairement proches de la borne
supérieure.
Proposition 1
Soit  une partie non vide de
une partie non vide de
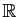 .
.
- Si
 est majorée, alors
est majorée, alors
- Si
 est minorée, alors
est minorée, alors
Démonstration : Comme 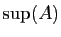 est le plus petit des majorants,
est le plus petit des majorants,
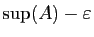 ne
peut pas être un majorant. Il existe donc un élément de
ne
peut pas être un majorant. Il existe donc un élément de  supérieur à
supérieur à
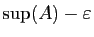 . Comme
. Comme 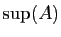 est un majorant, cet
élément est inférieur à
est un majorant, cet
élément est inférieur à 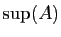 . Le raisonnement pour
. Le raisonnement pour
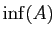 est analogue.
est analogue.
Nous allons souvent rencontrer dans ce cours des réels
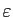 strictement positifs arbitrairement petits. On peut s'en faire une
idée concrète en pensant
strictement positifs arbitrairement petits. On peut s'en faire une
idée concrète en pensant
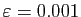 , ou bien
, ou bien
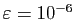 . Prenons comme exemple
. Prenons comme exemple
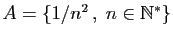 . La borne inférieure est
. La borne inférieure est 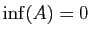 .
La proposition 1 permet d'affirmer que pour tout
.
La proposition 1 permet d'affirmer que pour tout
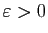 , il existe un élément de l'ensemble inférieur à
, il existe un élément de l'ensemble inférieur à
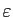 . Et d'ailleurs l'équivalence ci-dessous permet de l'exhiber.
. Et d'ailleurs l'équivalence ci-dessous permet de l'exhiber.
Pour
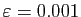 ,
,
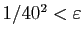 .
La proposition 1 admet la réciproque suivante.
.
La proposition 1 admet la réciproque suivante.
Démonstration : Si
alors pour tout
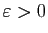 ,
,
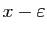 n'est pas un majorant de
n'est pas un majorant de  ,
donc si
,
donc si  est un majorant, c'est bien le plus petit.
Le raisonnement pour
est un majorant, c'est bien le plus petit.
Le raisonnement pour 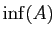 est analogue.
est analogue. La borne supérieure peut donc être caractérisée de deux
manières différentes.
La borne supérieure peut donc être caractérisée de deux
manières différentes.
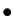
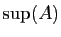 est le plus petit des majorants de
est le plus petit des majorants de 
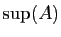 est le seul majorant
est le seul majorant  de
de  tel que pour tout
tel que pour tout
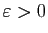 , il
existe un élément de
, il
existe un élément de  entre
entre
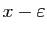 et
et  .
.
De manière analogue,
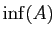 est le plus grand des minorants de
est le plus grand des minorants de 
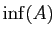 est le seul minorant
est le seul minorant  de
de  tel que pour tout
tel que pour tout
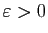 , il
existe un élément de
, il
existe un élément de  entre
entre  et
et
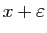 .
.
En liaison avec la proposition précédente, voici pour terminer
cette section une application simple
des notions de borne supérieure et inférieure, que
l'on retrouve dans beaucoup de démonstrations.
Proposition 3
Soient 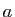 et
et 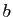 deux réels.
deux réels.
- Si pour tout
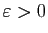 ,
,
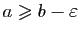 alors
alors
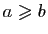 .
.
- Si pour tout
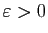 ,
,
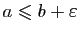 alors
alors
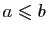 .
.
Démonstration : Considérons la première affirmation. l'ensemble
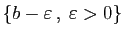 a pour borne supérieure
a pour borne supérieure
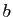 . L'hypothèse affirme que
. L'hypothèse affirme que 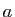 est un majorant de cet ensemble. Il
est donc supérieur ou égal à la borne supérieure, par définition
de celle-ci. Or d'après la proposition 2, la borne
supérieure de
est un majorant de cet ensemble. Il
est donc supérieur ou égal à la borne supérieure, par définition
de celle-ci. Or d'après la proposition 2, la borne
supérieure de
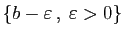 est
est 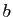 .
La seconde affirmation est analogue.
.
La seconde affirmation est analogue. 
L'ensemble
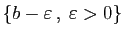 de la démonstration
précédente est un intervalle de
de la démonstration
précédente est un intervalle de
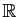 . Nous les décrivons
dans la section suivante.
. Nous les décrivons
dans la section suivante.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() strictement positifs arbitrairement petits. On peut s'en faire une
idée concrète en pensant
strictement positifs arbitrairement petits. On peut s'en faire une
idée concrète en pensant
![]() , ou bien
, ou bien
![]() . Prenons comme exemple
. Prenons comme exemple
![]() . La borne inférieure est
. La borne inférieure est ![]() .
La proposition 1 permet d'affirmer que pour tout
.
La proposition 1 permet d'affirmer que pour tout
![]() , il existe un élément de l'ensemble inférieur à
, il existe un élément de l'ensemble inférieur à
![]() . Et d'ailleurs l'équivalence ci-dessous permet de l'exhiber.
. Et d'ailleurs l'équivalence ci-dessous permet de l'exhiber.
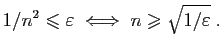
![]() de la démonstration
précédente est un intervalle de
de la démonstration
précédente est un intervalle de
![]() . Nous les décrivons
dans la section suivante.
. Nous les décrivons
dans la section suivante.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales