Nous ne présenterons pas de construction axiomatique de l'ensemble
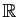 des nombres réels. Cette section rappelle
quelques notations, les propriétés des opérations
(addition, multiplication) et de la relation d'ordre.
des nombres réels. Cette section rappelle
quelques notations, les propriétés des opérations
(addition, multiplication) et de la relation d'ordre.
Nous utilisons les notations classiques
suivantes pour les ensembles emboîtés de nombres
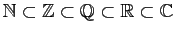 .
.
| Notation |
Ensemble |
Exemples |
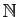 |
Entiers naturels |
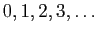 |
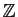 |
Entiers relatifs |
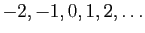 |
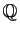 |
Rationnels |
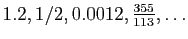 |
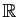 |
Réels |
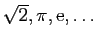 |
 |
Complexes |
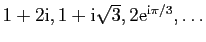 |
L'exposant 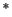 signifie «privé de 0». Ainsi,
signifie «privé de 0». Ainsi,
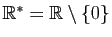 ,
,
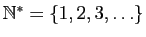 .
Pour les calculs usuels (à la main, sur les calculettes ou par
ordinateur), ce sont forcément des nombres décimaux, donc
rationnels, que l'on manipule. Pourtant l'ensemble
.
Pour les calculs usuels (à la main, sur les calculettes ou par
ordinateur), ce sont forcément des nombres décimaux, donc
rationnels, que l'on manipule. Pourtant l'ensemble
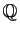 n'est pas un
cadre de calcul mathématiquement suffisant, pour plusieurs raisons,
qui seront énoncées dans la suite de ce chapitre. La première,
reconnue dès l'antiquité grecque,
est que certaines quantités, qui pourtant
apparaissent couramment en géométrie élémentaire, ne
s'expriment pas comme rapports d'entiers. La plus simple est la
diagonale d'un carré de côté
n'est pas un
cadre de calcul mathématiquement suffisant, pour plusieurs raisons,
qui seront énoncées dans la suite de ce chapitre. La première,
reconnue dès l'antiquité grecque,
est que certaines quantités, qui pourtant
apparaissent couramment en géométrie élémentaire, ne
s'expriment pas comme rapports d'entiers. La plus simple est la
diagonale d'un carré de côté 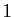 , à savoir
, à savoir 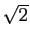 : nous
verrons plus loin que
: nous
verrons plus loin que 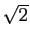 n'est pas un nombre rationnel;
n'est pas un nombre rationnel;
![$ \sqrt[3]{5}$](img17.gif) ,
, 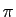 , ou
, ou
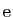 n'en sont pas non plus.
n'en sont pas non plus.
Les propriétés de l'addition, de la
multiplication et de la relation d'ordre sont rappelées ci-dessous.
Addition
- Associativité :
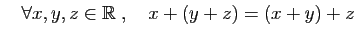
- Élément neutre :
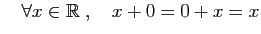
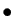
- Opposé :
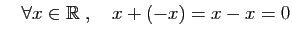
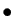
- Commutativité :
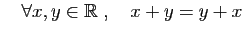
L'ensemble des réels muni de l'addition est un
groupe commutatif.
Multiplication
L'ensemble
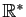 (ensemble des réels
privé de 0), muni de la multiplication, est un autre
groupe commutatif.
(ensemble des réels
privé de 0), muni de la multiplication, est un autre
groupe commutatif.
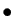
- Associativité :
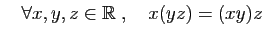
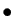
- Élément neutre :
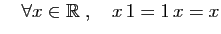
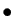
- Inverse :
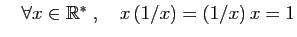
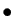
- Commutativité :
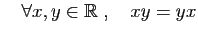
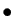
- Distributivité :
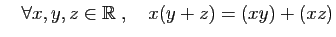
L'ensemble des réels muni de l'addition et
de la multiplication est un
corps commutatif.
Relation d'ordre
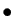
- Réflexivité :
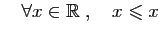
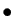
- Transitivité :
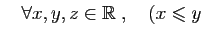 et
et 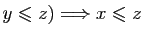
- Antisymétrie :
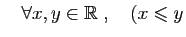 et
et 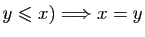
- Ordre total :
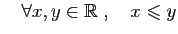 ou
ou 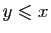
Les trois premières propriétés définissent une relation
d'ordre. Ici l'ordre est total car deux réels quelconques
peuvent toujours être comparés.
Pour des raisons de commodité, on utilise aussi couramment les notations
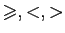 :
:
| Notation |
Définition |
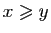 |
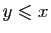 |
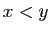 |
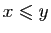 et et 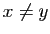 |
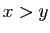 |
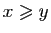 et et 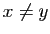 |
On utilise aussi les ensembles de réels notés
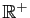 ,
,
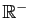 ,
,
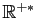 et
et
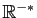 .
.
| Ensemble |
Définition |
Notation |
| Réels positifs ou nuls |
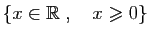 |
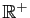 |
| Réels strictement positifs |
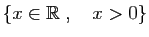 |
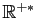 |
| Réels négatifs ou nuls |
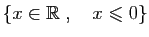 |
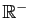 |
| Réels strictement négatifs |
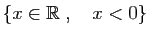 |
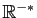 |
La relation d'ordre est compatible avec l'addition par un réel
quelconque, et avec la multiplication entre réels positifs.
-
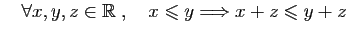
-
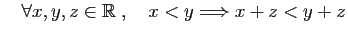
-
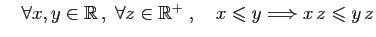
-
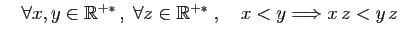
Comme conséquence de ces relations de compatibilité, on obtient
les règles suivantes qui permettent de combiner des inégalités.
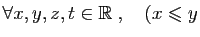
et
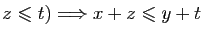
On peut donc ajouter deux inégalités de même sens (attention : on ne peut pas ajouter deux inégalités de sens
opposés ni soustraire deux inégalités de même sens).
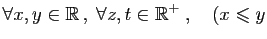
et
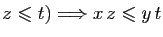
On peut multiplier deux inégalités de même sens, si elles concernent
des réels positifs ou nuls.
(attention : on ne peut pas mutiplier deux inégalités de sens
opposés, ni diviser des inégalités de même sens, ni multiplier
des inégalités qui concernent des réels négatifs).
Pour se ramener à des
inégalités de même sens, ou à des réels positifs, il peut
être utile de changer de signe ou de passer à l'inverse.
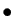
-
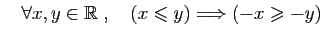
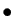
-
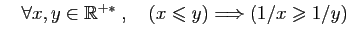
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() .
.
![]() (ensemble des réels
privé de 0), muni de la multiplication, est un autre
groupe commutatif.
(ensemble des réels
privé de 0), muni de la multiplication, est un autre
groupe commutatif.
![]() :
:
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales