Le mathématicien indien S. Ramanujan (1887-1920) a donné dans sa
courte vie beaucoup d'énoncés justes et très peu
d'explications sur sa démarche. Contrairement à
la légende, il n'a jamais affirmé :
Les trois nombres
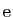 ,
, 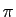 et
et
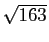 sont irrationnels. Il
n'est bien sûr pas exclu qu'en combinant des irrationnels on tombe
sur des rationnels ou même des entiers. L'exemple le plus
célèbre est celui de la formule d'Euler :
sont irrationnels. Il
n'est bien sûr pas exclu qu'en combinant des irrationnels on tombe
sur des rationnels ou même des entiers. L'exemple le plus
célèbre est celui de la formule d'Euler :
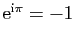 .
.
Il s'en faut de très peu que l'affirmation supposée de Ramanujan
soit vraie. Voici les 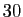 premiers chiffres significatifs
de
premiers chiffres significatifs
de
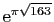 :
:
La partie entière a 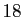 chiffres, et les
chiffres, et les 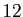 premières décimales
valent
premières décimales
valent 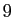 . Mais la treizième décimale vaut
. Mais la treizième décimale vaut 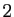 et le nombre n'est pas
entier. Ce fait était connu bien avant Ramanujan, par Hermite en
1859. Pourquoi alors le nombre
et le nombre n'est pas
entier. Ce fait était connu bien avant Ramanujan, par Hermite en
1859. Pourquoi alors le nombre
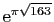 porte-t-il
le nom de «constante de Ramanujan» ?
À cause d'un poisson d'avril monté par M. Gardner en
1975 : on ne prête qu'aux riches !
porte-t-il
le nom de «constante de Ramanujan» ?
À cause d'un poisson d'avril monté par M. Gardner en
1975 : on ne prête qu'aux riches !
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() premiers chiffres significatifs
de
premiers chiffres significatifs
de
![]() :
:
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales